MIS CLASES - 6° Primaria Miércoles 14 de abril
La proporcionalidad en la vida diaria
Aprendizaje esperado: Comparación de razones en casos simples.
Énfasis: Resolver problemas de comparación entre dos razones igualando un término en ambas, duplicando o triplicando los términos de una de ellas.
¿Qué vamos a aprender?
En esta clase vas a realizar la comparación de razones en casos simples para ello deberás resolver problemas de comparación entre dos razones igualando un término en ambas, duplicando o triplicando los términos de una de ellas.
Realizarás algunas comparaciones entre cantidades e identificarás la relación que hay entre los valores a partir de duplicar o triplicar algunas cantidades. Vas a necesitar tu libro Desafíos sexto grado, tu cuaderno u hoja para tomar notas, lápiz, goma, sacapuntas y mucha disposición.

¿Qué hacemos?
Revisa los desafíos. Encuentra y registra las respuestas.
El primer desafío es el siguiente:

“Tengo dos cajas con pelotas. En la caja A hay 8 pelotas, tres son de color amarillo y 5 de color verde. En la caja B, hay 16 pelotas, 6 son amarillas y 10 son verdes”. ¿Cuál de las dos cajas me conviene usar para sacar una pelota amarilla?
Reflexiona… ¿Será la caja b, porque tiene más pelotas amarillas? Observa detenidamente las dos cajas. Se tiene la caja A y la caja B. Apóyate en la información que te brinda la imagen que representa la situación. ¿Cuántas pelotas en total hay en la caja A?
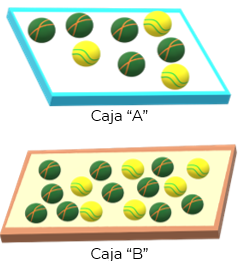
En la caja A hay 8 pelotas.
¿Cuántas pelotas en total hay en la caja B? En la caja B hay 16 pelotas.
Observa bien las imágenes, analiza el problema y anota tu respuesta. Es importante observar detenidamente las dos cajas y buscar alguna relación entre los datos.
¿Cuántas pelotas amarillas hay en la caja A? Hay 3 amarillas.
¿Cuántas pelotas verdes? Hay 5 pelotas verdes.
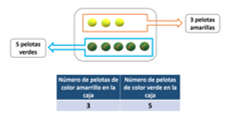
Observa los datos de la caja A, registrados en una tabla.

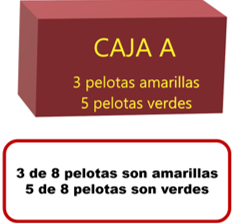
Hay 8 pelotas en total en la caja A. 3 de 8 pelotas son amarrillas y 5 de 8 son verdes.
Podría decirse que la relación entre ambos colores es que, por cada 3 pelotas amarrillas hay 5 pelotas verdes en la caja A.
Ahora si se quiere conservar la misma relación entre las pelotas de ambos colores y en otra caja se duplica la cantidad de pelotas amarillas, ¿cuántas pelotas verdes debería tener?
Puede resolverse así: si en la caja B hay el doble de amarillas que en la caja A, entonces tendría que duplicar también la cantidad de pelotas verdes, es decir, 2 veces 3, son 6 pelotas amarillas, y 2 veces 5 son 10 pelotas verdes.
¿Recuerdas cuantas pelotas de cada color tenía la caja B que menciona el problema?.
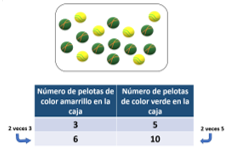
Observa los datos en la tabla y los datos de la caja B.
Es momento de usar la información obtenida y observar, qué ocurre, para dar respuesta a la pregunta, pues recordando el problema decía que la caja B tenía 6 pelotas amarillas y 10 verdes
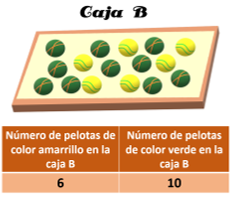
Comparándolo con los datos de la tabla, entonces al duplicar las cantidades de pelotas amarrillas y verdes de la caja A, se obtiene la misma cantidad de pelotas de cada color que hay en la caja B.
Ahora trabaja con las cantidades de la caja B, y recuerda lo que hiciste la sesión pasada, al analizar las características entre los conjuntos de cantidades cuando están en una situación de proporcionalidad directa.
Observas que, si es posible sacar el doble o el triple de ambas cantidades, también es posible obtener la mitad o la tercera parte. En este caso, ¿qué conviene obtener de ambas cantidades?

¿La mitad?... Sí, conviene la mitad. Y así se tiene que la mitad de 6 es 3 y corresponde a la cantidad de pelota amarrillas de la caja A. Y al obtener la mitad de 10, la cantidad de pelotas verdes, se tiene que es 5 y también corresponde a la caja A.

Esto también te permite ver que en las dos cajas existe la misma razón de pelotas amarillas y pelotas verdes.
Entonces, ¿cuál de las dos cajas conviene usar para sacar una pelota amarilla? ¿Da lo mismo una que otra? Así es, precisamente esa sería la conclusión: no importa de cuál de las dos cajas elijas, pues en ambas existe la misma razón entre pelotas amarrillas y verdes.
Ahora analiza esta situación.

En la imagen hay dos cajas, una de ellas ya la conoces, es la caja A, pero ahora está también la caja C. La pregunta es la misma de antes: ¿Cuál de las dos cajas conviene, si quiero sacar una pelota amarilla?
Observa los datos que aparecen en las cajas. Anota tu resultado y después podrás comparar. No olvides que siempre debes tener un argumento de por qué eliges una u otra respuesta. ¿Ya encontraste una solución?
Tal vez pienses que aquí si conviene más una caja, y es la caja C, porque tiene muchas más pelotas amarillas. Es importante realizar una comprobación de lo que se piensa. Así que analiza el planteamiento.
La caja A tiene 8 pelotas y la caja C tiene 16 pelotas.

¿Recuerda cuántas pelotas amarillas y verdes hay en cada caja, y expresa si la siguiente afirmación es verdadera o falsa: “En la caja A, 3 de 8 pelotas son amarrillas”.

Entonces, ¿cuál puede ser la afirmación para considerar las pelotas verdes en esa caja?

Muy bien- Pasa a la caja C. ¿Recuerdas cuántas pelotas hay en total?

Son 16 en total.¿Cuántas son de cada color? 10 de 16 pelotas son amarillas, y 6 de 16 pelotas son verdes. Se tienen 10 pelotas amarillas y 6 pelotas verdes.
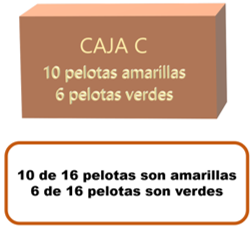
En la imagen está la relación de pelotas amarillas y verdes en cada caja.
Al comparar las pelotas amarillas con respecto del total que hay en cada caja, puedes ver que en la caja A, las pelotas amarillas son menos de la mitad del total que hay en la caja, en cambio, en la caja C, las pelotas amarillas son más de la mitad de total de pelotas de esa caja.
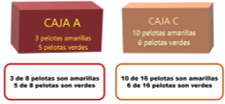
Entonces la respuesta correcta es que conviene más la caja C para sacar una pelota amarilla. Efectivamente, al establecer las relaciones entre el número de pelotas que hay en cada caja puedes ver que la caja que conviene usar es la caja C para sacar una pelota amarilla. Porque en la caja A, 3 de 8 pelotas son amarillas y en la caja C 10 de 16 pelotas con amarillas. Y, precisamente lo puedes observar en la siguiente imagen.
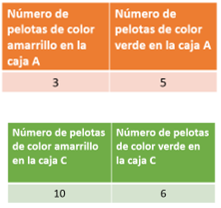
Ahí puedes observar la relación de pelotas de cada color en la caja A y en la caja C. Y al tratar de encontrar una cantidad de pelotas amarrillas común en ambas cajas para compararlas tenemos que...
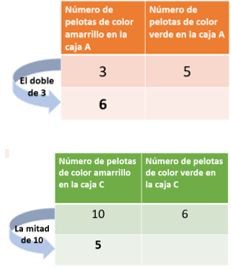
Al obtener el doble de 3 pelotas amarrillas en la caja A y la mitad de 10 pelotas amarrillas en la caja C no se encuentran valores en común que permitan comparar fácilmente, así que será necesario buscar otra estrategia.
¿Qué estrategia puede servir entonces? Recuerda lo que se hizo con las naranjas? Pues ahora realizarás algo semejante, duplicar o triplicar las cantidades de cada tabla hasta encontrar una cantidad común de pelotas amarillas. Entonces comenzarías obteniendo el doble de las cantidades que aparecen en ambas tablas, luego, el triple, y así sucesivamente hasta tener una cantidad en común.
De la misma forma como lo has hecho en las otras situaciones. Exactamente.

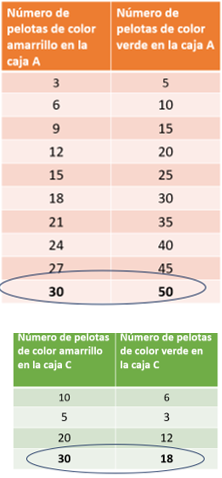
¿Ya observaste que 30 es el número común para ambas cajas y también que el valor que le corresponde de pelotas verdes en cada caso.
En la caja C la relación entre las pelotas amarrillas y las verdes es mucho mayor que en la caja A, lo que lleva a ratificar la respuesta. Ahora sí, ya sabes cómo comprobar por qué en una caja conviene más que en la otra sacar pelotas amarillas.
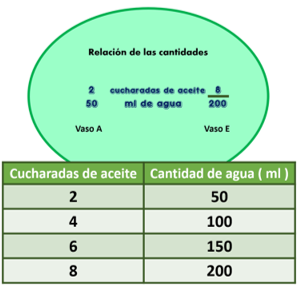
Ahora realiza un experimento con la asistencia de un adulto. En el vaso A hay 2 cucharadas de aceite por cada 50 ml agua. El vaso E tiene 8 cucharadas de aceite por 200 ml de agua. ¿Qué mezcla tiene mayor cantidad de aceite?
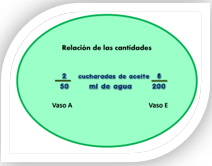
Analiza bien la información que proporciona el problema con respecto a las cantidades que tienen los dos vasos. Tal vez estás pensando que el vaso que tiene más aceite es el que tendría mayor concentración al mezclarlo.
En lo que piensas tu respuesta considera que si haces este experimento puedes observar claramente las sustancias en los vasos, por eso se eligió agua y aceite, pero en la vida cotidiana vas a encontrar mezclas en las que no podrás observar cada una de las sustancias que la componen, es decir, una de las sustancias se disuelve en la otra.
Utiliza una tabla para encontrar la respuesta. En la primera columna están las cucharadas de aceite y en la segunda columna la cantidad de agua.
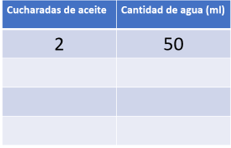
Como el problema dice: 2 cucharadas de aceite, las debes anotar y escribir 50 ml de agua en la otra columna
En la tercera fila vas a duplicar las cucharadas de aceite y la cantidad de agua son 100 ml de agua.
Luego 3 veces 2 cucharadas de aceite, que son 6 cucharadas de aceite y 3 veces 50 ml de agua son 150 ml de agua.
Después 4 veces 2 son 8 cucharadas de aceite y 4 veces 50 son 200 ml.
Con esos datos que encontraste, ¿a qué conclusión llegas? Ahora compruebas que ambos vasos tienen la misma proporción entre el aceite y el agua.
Con los datos que fuiste encontrando comprobaste que ambos vasos tienen la misma concentración de aceite con respecto del agua.
Piensa que el experimento que acabas de hacer está muy relacionado con el jabón líquido o el gel antibacterial que se usa mucho actualmente. No importa si compras una botella chica o grande, la mezcla tiene los ingredientes de forma proporcional. Compres poco o mucho de cualquiera de las dos mezclas que mencionas su efectividad es la misma. Únicamente cambia cuando compras una marca diferente, porque cada empresa tiene su propio procedimiento y cantidad de insumos que usa en su fórmula.
Piensa en otro ejemplo donde creas que se aplique lo que acabas de hacer con el aceite y el agua… ¿ya lo tienes?, ¿qué otro ejemplo se te ocurre?
Por ejemplo, cuando tu mamá prepara la comida, a veces usa recetas para hacer nuevos platillos. Y en la receta dice las cantidades a utilizar de cada ingrediente de acuerdo con las porciones que se vayan a preparar. La mayoría de las recetas dicen la cantidad de porciones que puedes obtener con la cantidad de ingredientes que te indican, por ejemplo, puede decir cuatro porciones. Si tu mamá quiere hacer esa receta para obtener 8 porciones ¿Qué es lo que debe hacer? Poner el doble de la cantidad de los ingredientes, por ejemplo, si dice 1 zanahoria, tendrá que poner 2 zanahorias, si dice media cucharada de aceite, tendrá que poner 1 cucharada.
Como te darás cuenta en diferentes actividades de la vida diaria hay ejemplos de este tema.
Analiza el problema del libro de texto, en la página 102, desafío 50 ¿Cuál está más concentrado?
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/102

Se preparó una naranjada A con 3 vasos de agua por cada 2 de jugo concentrado. Además, se preparó una naranjada B con 6 vasos de agua por cada 3 de jugo. ¿Cuál sabe más a naranja?
Observa y analiza los datos que te proporciona problema
Aquí está la jarra con la naranjada A, preparada con 3 vasos de agua por cada 2 de jugo concentrado y la naranjada B con sus correspondientes 6 vasos de agua por cada tres de jugo concentrado.

De acuerdo con lo que observas, ¿qué camino encuentras para llegar a la solución?¿cómo crees quese puede llegar a la respuesta?
En la jarra A, un vaso de concentrado de jugo con uno de agua, otro vaso de jugo con uno de agua, en la jarra A se agrega un vaso de agua más, pero no se agrega el jugo.

En la jarra B se agrega un vaso de jugo con uno de agua, otro vaso de jugo con un vaso de agua, otro vaso de jugo con su vaso de agua y se agregan 3 vasos más de agua.

¿Cuál es la conclusión de acuerdo con lo que realizaste?
Que la jarra A tiene más sabor a naranja. Porque en la jarra a hay únicamente un vaso de agua más y en la jarra B hay 3 vasos de agua y esto hace que sepa menos a naranja.
Es un buen camino para hacer el análisis, ¿de qué otra forma se puede comprobar si la conclusión es cierta?
¿Usando tablas?
Exacto, retoma la información, la naranjada A tiene 2 vasos de concentrado de jugo por 3 de agua, la naranjada B se preparó con 3 vasos de jugo concentrado y 6 vasos de agua.

¿Puedes obtener el doble? Y también la mitad del concentrado de la otra naranjada.
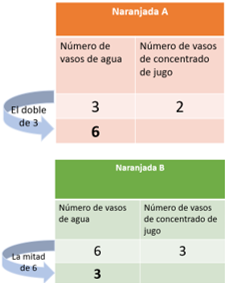
Ya puedes comparar y ver en cuál preparación tiene más concentrado de naranja.
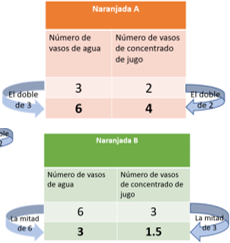
Con ese resultado puedes llegar a una conclusión. Ahora se puede hacer la comparación numérica de que en la naranjada A está más concentrado de naranja y, por tanto, sabe más a naranja.
Analiza el siguiente problema que plantea el libro de texto.
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/102

Como en el problema anterior se aplicaron dos procedimientos, quizá hayas encontrado alguna otra forma de llegar al resultado, así que trata de solucionar el problema.
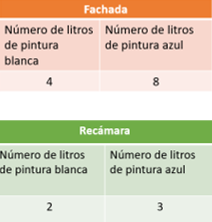
La cantidad de litros de pintura blanca en relación con la cantidad de los litros de pintura azul en la fachada es igual a 4 litros de pintura blanca por 8 de pintura azul.
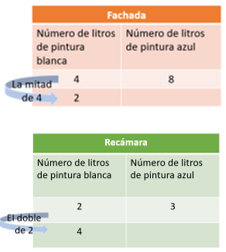
Y la relación de los litros de pintura que se usaron en la recámara es de 4 litros de pintura blanca por 6 litros de pintura de azul. ¿En qué mezcla hay más color azul?
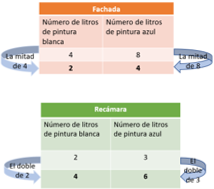
Pues en la mezcla para la fachada.
¿Qué te pareció el desafío de hoy? Seguramente nunca te habías detenido a pensar que en una receta se utilizara la proporción, un conocimiento matemático.
Así es, la relación de una cantidad con otra, la vas a encontrar en diversas situaciones de la vida cotidiana. Siempre tienes que analizar cómo se relacionan las cantidades para poder tomar decisiones acertadas, para ello puedes recurrir a imágenes y a fracciones equivalentes como lo hiciste el día de hoy para encontrar una respuesta.
Recuerda hay muchos caminos para llegar al resultado.
El Reto de Hoy:
Comparte lo que aprendiste respecto de las proporciones con alguien cercano, explícale los problemas que resolviste y como lo hiciste, seguramente le parecerá muy interesante.
Si te es posible, consulta otros libros y materiales para saber más sobre el tema. Si tienes la fortuna de hablar una lengua indígena aprovecha también este momento para practicarla y platica con tu familia en tu lengua materna.
¡Buen trabajo!
Gracias por tu esfuerzo.
¿De dónde vienen las leyes?
Aprendizaje esperado: Analiza críticamente si las normas de convivencia que se establecen en los diversos contextos a los que pertenece están sustentadas en principios éticos, la justicia y el bien común.
Énfasis: Comprende cómo surgen las leyes y cómo contribuyen a garantizar los derechos de las personas, la justicia y el bienestar colectivo.
¿Qué vamos a aprender?
Hoy tendrás la oportunidad de analizar de manera crítica si las normas de convivencia que se establecen en los diversos contextos a los que pertenece están sustentadas en principios éticos, la justicia y el bien común. En este ejercicio debes concentrarte en comprender cómo surgen las leyes y cómo contribuyen a garantizar los derechos de las personas, la justicia y el bienestar colectivo.
Recuerda tener a la mano hojas de papel, un cuaderno o una libreta, lápices o crayolas de colores, y un lápiz o pluma para escribir lo que te parezca relevante o interesante de la clase del día de hoy. También toma en cuenta que en esta sesión puedes emplear el libro de texto de Formación Cívica y Ética, Sexto Grado, en la página 110.
https://libros.conaliteg.gob.mx/20/P6FCA.htm#page/110

¿Qué hacemos?
Actividad 1
Realiza un repaso. Observa la imagen.

Recuerda que la sesión pasada aprendiste que las normas son indicaciones, principios o reglas que todos debemos seguir para convivir en armonía.
Aprendiste que las normas existen para regular el desarrollo de las sociedades y guiar la manera de conducirnos.
Las normas deben ayudarnos a defender nuestros derechos y cuidar de las y los demás.
Observaste también que hay que estar alerta cuando una norma no se aplica correctamente y dialogar con la autoridad correspondiente.
Aprendiste también que aunque haya situaciones que a veces parecen injustas, primero deben de revisarse las reglas y saber que todos y todas debemos participar para cumplirlas.
Estos conocimientos se relacionan con la imagen anterior pues en la imagen se trata de la mujer griega que representa a la Justicia. Tiene los ojos vendados, una balanza y una espada.
Esta mujer caracteriza tanto a la diosa griega Temis como a la diosa romana Justitia.
Tiene los ojos vendados, ya que esa acción representa que no le da preferencia a nadie. El objeto de la balanza, en donde se nivelan los pesos de ambos lados. Y una espada que representa la ejecución de las medidas.
Es importante que niños y niñas conozcan sus derechos. Y eso sucede, cuando se practica la justicia y entre todos y todas cuidamos y defendemos esos derechos.
Entonces, como aprendiste la sesión pasada, las normas y leyes sirven para que se cumplan y se respeten los derechos humanos. Toda norma tiene una razón de ser y cumple con el objetivo de hacer posible la convivencia al crear derechos comunes para todos y todas, y evitar actos de injusticia.
Y así como existen normas y reglas en el hogar, trabajo, en la calle, parque, centros comerciales, transporte público, entre otros espacios , también existen leyes para organizar a la sociedad en general, distribuir responsabilidades y orientar las conductas de las personas. Esto hará que una sociedad sea justa, libre y democrática.
En este país, la Constitución Política es la ley que organiza la convivencia de todas las personas en sociedad. La Constitución Política de los Estados Unidos Mexicanos, dice cómo se deben comportar todas las personas, como convivir juntos en este territorio y encontrar soluciones a los problemas comunes. También indica la manera como debe funcionar el gobierno.
Actividad 2
Conoce un poco más de ella por medio del video siguiente.
- Video: “Acuérdate de... Día de la Constitución Mexicana”.
https://www.youtube.com/watch?v=_gfLuTI4Bkk
Observa cuantas leyes hay para cuidar los derechos para vivir de forma organizada en sociedad. Los derechos humanos que la Constitución reconoce, están garantizados para todas las personas, las cuales sin excepción pueden pensar, decir, oír, escribir o hacer lo que deseen, siempre y cuando al hacerlo no dañen a los demás.
De eso se trata la justicia: “Dar a cada quien lo que le corresponde” porque más allá de una percepción individual, la idea de justicia se refiere a que todas las personas deben ser tratadas de la misma forma.
Para garantizar la justicia en una sociedad, es necesario que existan leyes escritas o codificadas que definan con toda claridad lo que una persona puede hacer o no en un país, es decir en un territorio específico.
Conoce un poco más de las leyes que nos rigen para identificar que ayudan a orientar los pensamientos y acciones de las personas; en la cultura popular hay muchos refranes que buscan el mismo objetivo.
Por ejemplo, el dicho “Donde manda capitán no gobierna marinero”. Ese es un dicho que pareciera una ley, “una persona no puede dar órdenes cuando tiene una autoridad o jefe”, pero es solo un dicho. Debes saber distinguirlos y saber que unos son solamente dichos mientras que las leyes sí se encuentran escritas y estipuladas para que todas y todos las cumplamos.
Actividad 3
La actividad consiste en jugar a la lotería.
Aparecerá una imagen y una frase. Tú debes decir si se trata de una ley o un refrán.

“Al pan pan, y al vino vino”. |
Significa que digamos las cosas como son y por su nombre, sin rodeos.
¿Es una ley o un refrán…?
¡Es un refrán!
¡Sigue adelante!
“Está prohibida la esclavitud en los Estados Unidos Mexicanos”. |
¿Es una ley o un refrán…?
¡Es una ley!
¡Sigue adelante!

“Los pueblos y comunidades indígenas tienen derecho a preservar y enriquecer sus lenguas originarias”. |
¿Es una ley o un refrán…?
¡Es una ley!
¡Sigue adelante!

“No hagas lo que no quieras que te hagan”. |
¿Es una ley o un refrán…?
¡Es un refrán! Es un refrán que nos enseña a tratarnos con respeto y dignidad.
¡Sigue adelante!

“La justicia es ciega”. |
¿Es una ley o un refrán…?
¡Es un refrán! Ese es un dicho, tiene que ver con lo que observaste de la imagen de la justicia.
¡Sigue adelante!

“Tenemos derecho a un medio ambiente adecuado para nuestro desarrollo”. |
¿Es una ley o un refrán…?
¡Es una ley!
¡Sigue adelante!

“Quien se fue a la Villa perdió su silla”. |
¿Es una ley o un refrán…?
¡Es un refrán! Es un refrán, y significa que oportunidades que no aprovechamos alguien más las puede aprovechar.
¡Sigue adelante!

“Quien parte y reparte se queda con la mejor parte” |
¿Es una ley o un refrán?
Ese es un refrán que hace referencia a que muchas veces cuando compartimos o repartimos algo nos quedamos con lo mejor para nosotros mismos.
¡Sigue adelante!

“Debe garantizarse el derecho de acceso a las tecnologías de la información y comunicación, incluido el internet”. |
¿Es una ley o un refrán…?
¡Es una ley!
Seguro que sí. Garantizar el acceso a las tecnologías de la información y comunicación incluido el internet para todas las personas es una ley muy importante para el desarrollo de nuestra sociedad.
Ahora reflexiona sobre ¿Por qué es necesario crear leyes?
Porque ellas nos dicen cómo deben ser los comportamientos y conductas de las personas, son las que dictan nuestros derechos y también nuestras obligaciones.
Pero si no conozco alguna ley o no me las sé todas ¿puedo entonces no cumplirlas? ¡De ninguna manera! Por eso las leyes siempre se encuentran escritas en documentos y soportes para que todas las personas podamos consultarlas y aunque no las conozcamos bien, tenemos, las personas y el gobierno, la obligación de cumplirlas porque si no es así, podemos dañar a alguien más.
Los seres humanos somos sujetos de derecho y eso nos garantiza tener la libertad de actuar, pensar y decidir, justamente como lo dicen nuestros derechos humanos, pero recordemos que vivimos en sociedad, y debemos interactuar con otras personas, por lo tanto tenemos límites que no podemos traspasar, porque podríamos estar dañando a alguien más, es decir violentando sus propios derechos y lastimando su dignidad.
Las leyes son muy importantes para que una sociedad pueda convivir. Son como los semáforos en las calles, para que podamos transitar sin que nos atropellen, hay que respetar los semáforos que organizan el tráfico.
Ahora preguntate si ¿las leyes se puedan modificar?
Sí, las leyes se pueden modificar, porque las personas y las sociedades van cambiando, las épocas no son las mismas, existen nuevos descubrimientos, estudios, nuevas formas de vida, costumbres, entre otros aspectos.
Recuerda algo que viste hace varias sesiones, por ejemplo, antes, las mujeres no tenían acceso al voto, y esa ley se cambió, y ahora es un derecho de toda la ciudadana. En este caso, puedes observar cómo la sociedad evolucionó y se dio cuenta de que su ley del voto no estaba completa y la cambió.
Revisa ahora cómo se originan las leyes.
- Video: “¿Cómo se origina una ley?”.
https://www.youtube.com/watch?v=JGQWq8YGTr4
Seguro te diste cuenta que para que un proyecto de ley, se convierta en ley, primero debe presentarse como una iniciativa y luego si ésta es aprobada, se convierte en ley. Así es, y entre los aspectos que se deben tomar en cuenta son los siguientes:

- Ideas y costumbres de una comunidad.
- Nuevas necesidades.
- Leyes ya existentes y formas de interpretarlas.
Investiga sobre una ley que se haya creado considerando los aspectos señalados. Será un gran trabajo para seguir informándote sobre las leyes que existen en nuestro país, porque como sabes, las leyes son necesarias para el buen funcionamiento de la sociedad, pues en ellas se garantizan tus derechos, además de que te ayudan a saber la forma en la que debes conducirte y actuar.
El Reto de Hoy:
Comparte con alguien cercano el valor que tiene el respeto y aplicación de las leyes que rigen a la sociedad mexicana, para fomentar la justicia, los derechos y las obligaciones de todos los ciudadanos.
Si te es posible, consulta otros libros y materiales para saber más sobre el tema. Si tienes la fortuna de hablar una lengua indígena aprovecha también este momento para practicarla y platica con tu familia en tu lengua materna.
¡Buen trabajo!
Gracias por tu esfuerzo.
El inicio del borrador de la carta de opinión.
Aprendizaje esperado: Expresa por escrito su opinión sobre hechos.
Redacta el borrador de una carta de opinión.
Adapta el lenguaje escrito para dirigirse a un destinatario.
Énfasis: Redacta borradores de cartas de opinión en las que se introduzcan argumentos suficientes sobre el tema comentado.
Valora la diversidad lingüística y cultural de México y escribe una carta de opinión que considere al destinatario.
¿Qué vamos a aprender?
Aprenderás a redactar borradores de cartas de opinión en las que utilices argumentos suficientes sobre el tema que hayas elegido, considerando un lenguaje acorde al destinatario de tu carta de opinión.
¿Qué hacemos?
En esta sesión iniciarás con la lectura.
Actividad 1
Realiza la lectura “Las vísperas del Fausto”, del autor argentino Adolfo Bioy Casares.
Las vísperas del Fausto
Adolfo Bioy Casares
“Esa noche de junio de 1540, en la cámara de la torre, el doctor Fausto recorría los anaqueles de su numerosa biblioteca. Se detenía aquí y allá; tomaba un volumen, lo hojeaba nerviosamente, volvía a dejarlo.

Por fin escogió los Memorabilia de Jenofonte. Colocó el libro en el atril y se dispuso a leer.

Miró hacía la ventana. Algo se había estremecido afuera. Fausto dijo en voz baja: “Un golpe de viento en el bosque.”

Se levantó, apartó bruscamente la cortina. Vio la noche, que los árboles agrandaban. Debajo de la mesa dormía Señor. La inocente respiración del perro afirmaba, tranquila y persuasiva como un amanecer, la realidad del mundo.

Fausto pensó en el infierno. Veinticuatro años antes, a cambio de un invencible poder mágico, había vendido su alma al Diablo. Los años habían corrido con celeridad. El plazo expiraba a media noche. No eran, todavía, las once. Fausto oyó unos pasos en la escalera; después, tres golpes en la puerta. Preguntó: “¿Quién llama?” “Yo”, contestó una voz que el monosílabo no descubría, “Yo.”

El doctor la había reconocido, pero sintió alguna irritación y repitió la pregunta. En tono de asombro y de reproche contestó su ayudante: “Yo, Wagner.” Fausto abrió la puerta. El ayudante entró con la bandeja, la copa de vino del Rin y las tajadas de pan y comentó con aprobación risueña lo adicto que era su amo a ese refrigerio. Mientras Wagner explicaba, como tantas veces, que el lugar era muy solitario y que esas breves pláticas lo ayudaban a pasar la noche, Fausto pensó en la complaciente costumbre, que endulza y apresura la vida, tomó unos sorbos de vino, comió unos bocados de pan y, por un instante, se creyó seguro. Reflexionó: Si no me alejo de Wagner y del perro no hay peligro.

Resolvió confiar en Wagner sus terrores. Luego recapacitó: Quién sabe los comentarios que haría. Era una persona supersticiosa (creía en la magia), con una plebeya afición por lo macabro, por lo truculento y por lo sentimental. El instinto le permitía ser vívido; la necedad, atroz. Fausto juzgó que no debía exponerse a nada que pudiera turbar su ánimo o inteligencia. El reloj dio las once y media. Fausto pensó: “No podrán defenderme. Nada me salvará.”

Después hubo como un cambio de tono en su pensamiento; Fausto levantó la mirada y continuó: “Más vale estar solo cuando llegue Mefistófeles. Sin testigos, me defenderé mejor.” Además, el incidente podía causar en la imaginación de Wagner (y acaso también en la indefensa irracionalidad del perro) una impresión demasiado espantosa. “Ya es tarde, Wagner. Vete a dormir.”

Cuando el ayudante iba a llamar a Señor, Fausto lo detuvo y, con mucha ternura, despertó a su perro. Wagner recogió en la bandeja el plato del pan y la copa y se acercó a la puerta. El perro miró a su amo con ojos en que parecía arder, como una débil y oscura llama, todo el amor, toda la esperanza y toda la tristeza del mundo. Fausto hizo un ademán en dirección a Wagner, y ambos salieron. Cerró la puerta y miró a su alrededor. Vio la habitación, la mesa de trabajo, los íntimos volúmenes. Se dijo que no estaba tan solo. El reloj dio las doce menos cuarto. Con alguna vivacidad, Fausto se acercó a la ventana y entreabrió la cortina. En el camino a Finsterwalde vacilaba, remota, la luz de un coche. ¡Huir en ese coche!, murmuró Fausto y le pareció que agonizaba de esperanza. Alejarse, he ahí lo imposible. No había corcel bastante rápido ni camino bastante largo. Entonces, como si en vez de la noche encontrara el día en la ventana, concibió una huida hacia el pasado; refugiarse en el año 1440; o más atrás aún: postergar por doscientos años la ineludible medianoche. Se imaginó al pasado como una tenebrosa región desconocida; pero, se preguntó: “Si antes no estuve allí, ¿cómo puedo llegar ahora?” ¿Cómo podía él introducir en el pasado un hecho nuevo? Vagamente recordó un verso de Agatón, citado por Aristóteles: “Ni el mismo Zeus puede alterar lo que ya ocurrió.” Si nada podía modificar el pasado, esa infinita llanura que se prolongaba del otro lado de su nacimiento era inalcanzable para él.

Quedaba, todavía, una escapatoria: Volver a nacer, llegar de nuevo a la hora terrible en que vendió el alma a Mefistófeles, venderla otra vez y cuando llegara, por fin, a esta noche, correrse una vez más al día del nacimiento.

Miró el reloj. Faltaba poco para la medianoche. Quién sabe desde cuándo, se dijo, representaba su vida de soberbia, de perdición y de terrores; quién sabe desde cuándo engañaba a Mefistófeles. ¿Lo engañaba? ¿Esa interminable repetición de vidas ciegas no era su infierno? Fausto se sintió muy viejo y muy cansado. Su última reflexión fue, sin embargo, de fidelidad hacia la vida; pensó que, en ella, no en la muerte, se deslizaba, como un agua oculta, el descanso. Con valerosa indiferencia postergó hasta el último instante la resolución de huir o de quedar. La campana del reloj sonó.
Fuente: Bioy Casares, Adolfo. “Las vísperas del Fausto”. Historia prodigiosa. Buenos Aires: Emecé, 1961, pp. 165-168.
¿Qué te pareció la lectura?
Quizá te recuerde el libro de Fausto, de Goethe, el cual está basado en otro de Marlowe, llamado La trágica historia del doctor Fausto, publicado en 1620.

En esta sesión complejizarás el esquema de planeación de la carta de opinión que se inició la sesión pasada, e iniciarás la escritura del borrador.
Los materiales que requerirás son: Libro de Texto, diccionario, cuaderno, y lápiz o pluma para escribir. Es muy importante que tengas a la mano tu diccionario, recuerda tenerlo cerca, durante esta sesión y también al leer o al estudiar otras asignaturas. Úsalo con libertad y no sólo investigues en torno a las palabras que aquí se solicitan.
¿Una carta de opinión utiliza un lenguaje formal o informal? ¿Por qué?
Formal, porque está dirigida al director de una publicación, al autor de un artículo o a la sociedad en general, con el propósito de compartir una opinión sobre determinado tema o hecho noticioso.
¿Coincides con esta respuesta? Ahora, según lo que se ha trabajado, ¿consideras que es un texto periodístico? ¿Por qué?
No, porque, aunque está hecho para publicarse en periódicos o revistas, no es un tipo de texto que sea propio del periodismo, sino un espacio que las publicaciones brindan a los lectores para que estos puedan expresarse.
Antes de continuar, lee un artículo de la Convención Americana de los Derechos Humanos.

Este es un artículo muy importante, considéralo al escribir tu carta de opinión, y de lo que has aprendido, ¿qué otras cosas necesitas tomar en cuenta para escribir tu carta de opinión?






Comentarios
Publicar un comentario