MIS CLASES - 6° Primaria Martes 11 de mayo
Canciones, adivinanzas y rimas tradicionales mexicanas
Aprendizaje esperado: Reflexiona en torno a diferentes manifestaciones culturales y lingüísticas de México.
Énfasis: Conoce y aprecia la diversidad lingüística y cultural de México.
Reflexiona sobre algunas expresiones literarias de las tradiciones mexicanas (canciones, adivinanzas, rimas).
¿Qué vamos a aprender?
Conocerás y apreciarás la diversidad lingüística y cultural de México y reflexionarás sobre algunas expresiones literarias de las tradiciones mexicanas como las canciones, adivinanzas y rimas, entre otras. Hoy comenzarás a trabajar con la práctica social del lenguaje 11. Conocer una canción de los pueblos originarios de México.
Actividad 1
Abre tu libro de texto de Español en la página 137 para que leas el propósito de la práctica social del lenguaje 11
https://libros.conaliteg.gob.mx/20/P6ESA.htm#page/137

El propósito de esta práctica social del lenguaje es que conozcas y aprecies la tradición oral de los pueblos originarios de México a través de canciones indígenas y expresiones literarias como la rima y las adivinanzas.
El trabajo se centrará en canciones lo cual resulta particularmente atractivo. Ni qué decir de las rimas y las adivinanzas, con las cuales podrás divertirte mucho y profundizarás en el conocimiento de una parte de la herencia cultural: La relativa a algunas expresiones de la tradición oral de los originarios de México, sobre todo las canciones.
EL propósito de esta sesión es conocer y reflexionar en torno a diferentes manifestaciones culturales y lingüísticas de México; en particular, leerás y trabajarás con varias expresiones literarias de las tradiciones mexicanas populares.
Los materiales que vas a necesitar son: cuaderno, libro de texto de Español, algo con que anotar y, de ser posible, un diccionario; recuerda tenerlo siempre a la mano, durante esta clase y también al leer o al estudiar otras asignaturas. Úsalo con libertad y no sólo investigues sobre las palabras que se emplean aquí. Piensa que el conocimiento profundo
Busca en el diccionario la palabra “tumbaburros”.
Tumbaburros
(Festival México) Diccionario.
Entonces, el “tumbaburros” es una manera festiva de llamar al diccionario en México.
Actividad 2
Lee el texto literario que refiere a la tradición oral mexicana. Comenzarás con unas adivinanzas; seguirás con una calavera literaria, unos letreros de camión y algunos versos empleados para cantar los naipes de la lotería; concluirás con una canción mixe.
Hoy sólo trabajarás con textos de la tradición popular.
Primero lee un par de adivinanzas de los siglos XVIII y XIX surgidas de la gente que habitaba este país en ese entonces, por esos años, igual que ahora, ya era un México diverso y poseía, sobre todo, sangre indígena, española y africana.

Como suele ocurrir con las adivinanzas, las pistas las otorga la adivinanza misma. ¿Qué clase de objeto cotidiano parece que camina en compás, con el pico por delante y los ojos detrás? Es muy visual.
Las tijeras.
|
|
Segunda adivinanza.

Igual que la adivinanza anterior, las pistas te las ofrece la adivinanza misma, si te fijas con calma, verás que no es menos visual.
Se trata de algo redondo.

Se trata de algo redondo que comparte varias palabras de la adivinanza.
La respuesta es la letra “o” las palabras “dios” y “pontífice” la incluyen, a diferencia de “papas” y “cardenales”.
Las dos adivinanzas que acabas de leer fueron tomadas de:
Referencia bibliográfica:
|
Como puedes observar, la referencia bibliográfica menciona al compilador, no al autor de las adivinanzas, esto se debe a que por ser textos pertenecientes a la tradición oral, suelen ser del dominio popular y carecen de un autor definido.
Ocurre lo mismo con otra clase de textos que ya has estudiado en otros grados, por ejemplo, las leyendas y los refranes.
Ahora vas a leer una adivinanza más, esta sí tiene autor. Como el libro del que fue extraída no lo explicita, se ignora si el autor la inventó o si la escuchó en su comunidad y luego la registró.
Como con las primeras adivinanzas, esta surge de la tradición oral y terminó formando parte de la tradición escrita, cuyo autor es Marcelino García López, quien, cuando la escribió tenía 12 años y vivía en Xochistlahuaca, Guerrero. Además, es importante que sepas que fue escrita originalmente en lengua amuzgo, hablada por el pueblo homónimo: amuzgo, que habita los estados de Guerrero y Oaxaca.
|
|
Quizá para los y las estudiantes de la región del sureste del país será más sencillo contestarla, sobre todo para el pueblo amuzgo, porque la conocen o porque están más familiarizados con las referencias culturales y naturales a las que se alu
El hecho de no conocer más sobre el pueblo amuzgo, ni sobre la región que habitan limita las posibilidades de responder, debido a que no se tienen los mismos referentes que quienes la crearon y la transmitieron.
Esta adivinanza también ofrece pistas, pero el hecho de desconocer los referentes culturales y naturales del pueblo amuzgo, se limitan las posibilidades de responderla, al menos de forma tan veloz. Las pistas son: Se trata de dos elementos de la naturaleza, uno negro y otro amarillo.
|
|
Los frijoles negros y los chipiles, que son las plantas que puedes ver en pantalla, las cuales forman parte de la familia de las leguminosas, como los frijoles, y también se emplean en la cocina. En Chiapas y en Tabasco el chipil es denominado chipilín.
¿Has probado la sopa y los tamales de chipilín? ¿Conocías la flor del chipilín? Muy difícil responder a la adivinanza si no conoces la flor.
La adivinanza que acabas de leer, fue escrita por Marcelino García López y fue extraída de la siguiente referencia bibliográfica:
González Parada, Ivette (compiladora) Las narraciones de niñas y niños indígenas, tomo II, México, SEP, 2001 p. 21
Ahora, realiza la lectura de corrido, de la calavera literaria anunciada, los letreros de camión y los versos para cantar los naipes de la lotería.


Los versos que acabas de leer, fueron extraídos de la siguiente referencia bibliográfica.
Zaid, Gabriel (presentación, compilación y notas) Ómnibus de poesía mexicana, 11ª edición, México, Siglo XXI editores, 1984 pp. 311-312, 293 y 310
¿Qué te parecieron estos textos?
Seguro te resultaron muy simpáticos, podrás notar de manera particular el ingenio y los juegos de palabras; por ejemplo, en los versos para cantar los naipes de la lotería: “Tiene roto el calcetín / el presumido CATRÍN”.
Son textos muy ingeniosos y simpáticos que, igual que las adivinanzas, hablan sobre la cultura a la que pertenecen. ¿Por qué crees que se te pidió que los leyeras de corrido? ¿Qué tienen en común?
Tienen un origen popular; no hay un autor definido; la manera principal en que se transmiten, es decir, la oralidad y la rima. ¿Recuerdas qué es la rima?
La rima refiere a la repetición de sonidos, entre dos o más versos, a partir de la última vocal acentuada. Existen la rima asonante y la rima consonante.
En la rima asonante sólo se repiten los sonidos de las vocales, como en: “La panza que ella tenía / no era empacho de SANDÍA” mientras que en la rima consonante se repiten los sonidos de las vocales y de las consonantes, como en: “El que espera / desesPERA".
Estos dos tipos de rimas los puedes encontrar en múltiples textos de origen popular.
En la rima asonante sólo se repiten los sonidos de las vocales y aunque no todos los textos de este tipo la emplean necesariamente, su uso es muy común, pues, entre otras cosas, la repetición de sonidos similares contribuye a la creación del ritmo y de cierto efecto musical.
Llegó el momento de trabajar con una canción: el “Himno mixe”, también conocido como “Himno a Kong Oy” o “Himno a Konk Ëy”, para ello, observa con atención el siguiente video. Mientras lo observas, disfruta y trata de identificar de qué habla la letra.
- Video del Centro de capacitación musical y desarrollo de la cultura mixe.
¿Qué opinas de la canción y de la manera de tocar de la orquesta del Centro de Capacitación Musical y Desarrollo de la Cultura Mixe (CECAM)?
A continuación leerás la letra de la canción en español.
Himno a Konk Ëy
¡Oh! Gran señor Konk Ëy,
rey de los mixes sois.
Tú bastón, gran señor,
lo clavaste en el tule.
¡Oh! Gran señor, padre y señor,
nos enseñaste a luchar.
¡Oh! Gran señor, padre y señor,
nos enseñaste a luchar.
Después de la quemazón,
subiste los picachos.
El cerro del Cempoaltépetl,
nos guarda tu memoria.
¡Oh! Gran señor, padre y señor,
nos enseñaste a luchar.
¡Oh! Gran señor, padre y señor,
nos enseñaste a luchar.
¿Sobre qué trata la canción?
El himno habla sobre un señor muy importante llamado Konk Ëy, quien es rey de los mixes y quien, por algún motivo, clavó su bastón en un árbol de tule. Al parecer fue un gran líder guerrero y sugiere que hubo una quemazón en el cerro del Cempoaltépetl y que ahí falleció su cuerpo. Sin embargo, como en el caso de la adivinanza sobre los chipiles y los frijoles, hay muchas cosas que sin contexto, es difícil comprender. El desconocimiento de la cultura mixe pudiera impedir entender con mayor profundidad la letra de la canción.
El desconocimiento de algo constituye siempre un buen motivo para el conocimiento. Por ello, con el objetivo de profundizar un poco más en el asunto, observa una breve cápsula sobre el tema; se titula “El origen del árbol del tule / El rey Kong Oy”, y explica el mito del rey Kong Oy al que hace referencia la canción.
- Video. El origen del árbol del tule. El rey Kong Oy.
Para profundizar en la comprensión tanto de la canción como del significado que posee para los mixes, será necesario investigar mucho más.
La responsabilidad de preservar las culturas y las lenguas es de todas y todos. La mejor manera de hacerlo es conocerlas y reconocerlas como propias, porque lo son, y enriquecerse y disfrutar de y con ellas. Para ahondar en el asunto, dialoga con tus familiares.
Las siguientes preguntas pueden servirte de guía:
- ¿Qué significa el hecho de que México sea un país pluricultural?
- ¿Qué culturas y lenguas existen en tu región?
- ¿Qué palabras en lengua indígena conoces?
- ¿Qué canciones, adivinanzas, rimas y/o poemas en lengua indígena has leído o escuchado?
Recapitulando lo aprendido.
Conocí y reflexioné en torno a diferentes manifestaciones culturales y lingüísticas de México; en particular, leí y reflexioné sobre varias expresiones literarias de las tradiciones mexicanas populares: tres adivinanzas, una calavera literaria, algunos letreros de camión, varios de los versos empleados al cantar los naipes de lotería, y una canción mixe: el “Himno a Konk Ëy”.
El Reto de Hoy:
Realiza la entrevista a alguno de tus familiares cercanos, con base en las preguntas anteriores, y registra las respuestas en tu cuaderno, seguramente conocerás datos muy importantes. Identifica la rima en algunas canciones que se escuchan en tu comunidad.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema. Si tienes la fortuna de hablar una lengua indígena aprovecha también este momento para practicarla y platica con tu familia en tu lengua materna.
¡Buen trabajo!
Gracias por tu esfuerzo.
¡Gira, que gira!
Aprendizaje esperado: Compara los efectos de la fuerza en el funcionamiento básico de las máquinas simples y las ventajas de su uso.
Énfasis: Identifica las características y aplicaciones de máquinas simples en la vida cotidiana: rueda y polea.
¿Qué vamos a aprender?
Aprenderás a comparar los efectos de la fuerza en el funcionamiento básico de las máquinas simples y las ventajas de su uso, así también podrás identificar las características y aplicaciones de máquinas simples en la vida cotidiana, en concreto de la rueda y la polea. Debes tener listo tu cuaderno de notas y tu lápiz, así como tu libro de texto de Ciencias Naturales, en la página 104
https://libros.conaliteg.gob.mx/20/P6CNA.htm?#page/104

¿Qué hacemos?
Para comenzar, pregúntate, ¿Cómo moverías una caja muy pesada? Para hacerlo la mejor solución te la ofrece una máquina simple.
Realiza un ejercicio de “relación de columnas”.
Observa la siguiente columna con las definiciones y funciones de las máquinas simples y otra columna con los ejemplos: palanca, cuña, plano inclinado y tornillo.
Transforma una fuerza vertical en dos fuerzas horizontales. | Cuña. |
Cuanto más pequeño sea su ángulo, más peso se podrá elevar con la misma fuerza aplicada. | Plano inclinado. |
Transforma un movimiento giratorio en uno rectilíneo. | Tornillo. |
Funciona con un punto de apoyo, llamado fulcro. | Palanca. |
Observa la primera descripción.
“Transforma una fuerza vertical en dos fuerzas horizontales”
Una pista es que la usamos para partir un objeto con más facilidad. Es la “cuña”. Une con una línea la definición y el nombre de esta máquina simple.
Ahora la siguiente:
“Cuanto más pequeño sea su ángulo, más peso se podrá elevar con la misma fuerza aplicada”
Analiza, “Cuanto más pequeño sea su ángulo.” ¿Cuál de las máquinas simples que has visto hasta ahora tiene un ángulo, es decir una inclinación? El plano inclinado. Une con una línea la definición y el nombre de esta máquina simple.
¿Qué quiere decir la frase? Pues que cuando movemos objetos en el plano inclinado, cuanta menos inclinación tenga este, más peso podremos mover con la misma fuerza. Pero se recorrerá más distancia. En cambio, si el ángulo es muy pronunciado, la distancia es más corta, pero se necesitará más fuerza para mover el objeto.
Continua con el que sigue:
“Transforma un movimiento giratorio en uno rectilíneo”
Una pista es que un sacacorchos funciona con el mismo principio de esta máquina simple. ¡Un tornillo! y por lo tanto, esta otra opción “Funciona con un punto de apoyo, llamado fulcro” corresponde a la palanca. Une con una línea las definiciones y los nombres de estas máquina simples.
Ahora, ¿Recuerdas las palabras de un científico griego, acerca de las máquinas simples, y específicamente sobre la palanca? Dice:
“Dadme un punto de apoyo y moveré al mundo”.
Lo dijo Arquímedes, pero ¿A qué crees que se refiere esa frase? Bueno, puede parecer una frase exagerada, pero a lo que se refería Arquímedes, es que la fuerza verdaderamente se puede amplificar en gran medida con el uso de la palanca, o de las otras máquinas simples. Esta famosa frase se refiere a que no hay límites para la amplificación de fuerza que nos proporciona esta “ventaja mecánica” de la máquina simple.
“VENTAJA MECÁNICA = CUÁNTO SE AMPLIFICA UNA FUERZA” |
La ventaja mecánica es una medida que indica cuánto se amplifica la fuerza usando una máquina simple, una herramienta o un dispositivo mecánico más complejo. Entonces, puede decirse que tanto el plano inclinado, como la palanca, el tornillo y la cuña, proporcionan una “ventaja mecánica”.
Al igual que las dos máquinas simples que veremos hoy: La rueda y la polea.
Piensa un poco, ¿Cuál crees que fue la primera máquina simple en utilizarse? Para que te des una idea, es una que, si te fijas bien, está por todas partes y, es difícil imaginar un mundo sin ella, su invención data de hace unos 7000 años.
Las primeras civilizaciones ya usaban algunas, la clase pasada, viste que los egipcios ya conocían el plano inclinado, y los griegos, gracias a Arquímedes, conocían la palanca, es probable que antes ya se usaba la rueda.
Precisamente, la rueda, es una de las máquinas simples que más se han usado hasta nuestros días. ¿Y se sabe quién la inventó? Se le atribuye su invención a la civilización mesopotámica, alrededor del año 5000 antes de nuestra era.

¿Recuerdas el trabajo que te cuesta jalar una caja? Eso se debe no sólo a la cantidad de material, sino también a la fricción de la caja contra el piso. Si la hubieras puesto en una mesa con ruedas, habría sido más sencillo moverla. El contacto entre una rueda y la superficie es muy pequeño, lo que permite mover la carga con poco esfuerzo, ya que la fricción se reduce.
¿Entonces una rueda en un eje sería otra máquina simple? No precisamente, la rueda es la base de varias máquinas simples, como el torno o la polea, que se abordarán más adelante, por ahora lo importante es entender qué es el eje de la rueda.
Un eje es una pieza con forma de cilindro que se ubica en el centro de la rueda. El eje puede girar junto con la rueda, como sucede, por ejemplo, en algunos mecanismos que hacen funcionar las manijas redondas de las puertas.
Pero hay otros casos, en los que las ruedas giran alrededor del eje, pero el eje no se mueve. Como en las ruedas de una carreta. Si hubieras tenido una carretilla o un “diablito” para cargar la caja, la habría traído aquí sin tanto problema.
Hablando de esa caja que arrastraste, ¿Cómo crees que se movería con más facilidad? es decir con menos esfuerzo, ¿En un carro con ruedas grandes, como esos triciclos donde llevan el pan? ¿O en un carro con ruedas pequeñas, como los de supermercado?
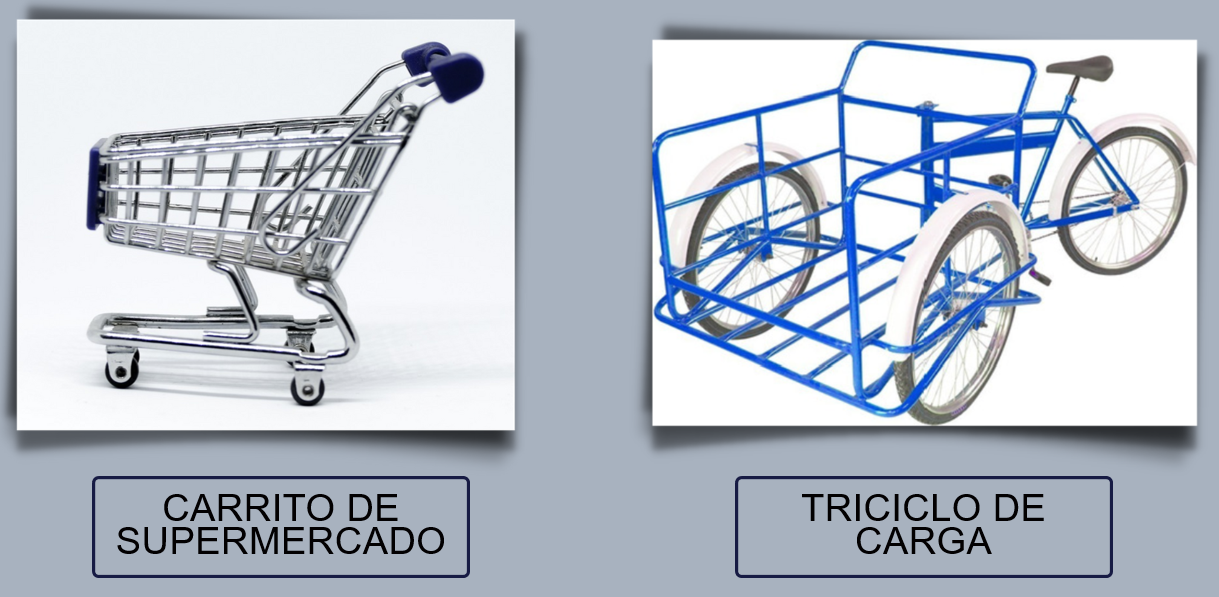
¿Por qué no haces una prueba? Con las ruedas grandes se recorre mayor distancia en un solo giro del eje que con las ruedas pequeñas. ¿Por qué? porque el perímetro en la rueda grande es mayor y recorre más distancia con un solo giro, además, el área que está en contacto con el suelo es mucho menor, en comparación con una rueda pequeña, que tiene que girar más veces para recorrer la misma distancia, por lo tanto, en una rueda grande la fricción es menor que en una pequeña.

Fuente: Jensen, N. (s/a) Máquinas simples y complejas. Recuperado el 25 de abril de 2021, de Sciencea-z. Sitio web: https://www.sciencea-z.com/content/samples/machines_3-4_nfbook_spanish_-_low.pdf
¿Ahora entiendes por qué en los medios de transporte terrestres encuentras tantas ruedas? La fuerza aplicada equivale a movimiento casi sin fricción, mejor dicho, con una fricción reducida, que se reduce aún más con el uso de polvo o aceites lubricantes.
Te preguntarás si el primer uso que se le dio a las ruedas, ¿Fue para el de transporte? En realidad, no. Al parecer, el primer registro que se tiene de una rueda no fue para una carreta o para un carro, sino el de una rueda de alfarería, que también conocemos como torno.
Se trataba de una máquina simple en la que dos ruedas estaban unidas por un eje. Sobre una de ellas se colocaba el barro que se iba a modelar, y la otra se hacía girar con el impulso de las piernas. Es un instrumento antiquísimo, que todavía se utiliza hoy en día. Observa esta máquina simple tan ligada a la elaboración de cerámica, en el siguiente video.

- Video. D Todo – Taller de cerámica.

Las ruedas son los objetos que usamos para movernos sobre una superficie.
Esos son usos que se le dieron desde la antigüedad, como ya has visto en otras sesiones: Los molinos de viento y los molinos de agua, son ruedas con palas o con aspas.
En la actualidad, ese movimiento rotativo puede ayudar a generar energía, aquí viene otro uso que hasta el momento no se había mencionado.

Y aquí vale la pena ilustrar bien esta aplicación que tiene la rueda. Si tienes una rueda puesta contra otra, cuando hacemos girar a una, la otra gira en dirección contraria.
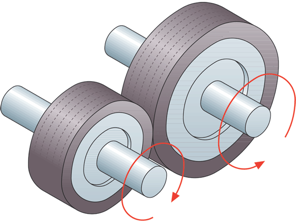
Con este principio, funcionan las poleas (que son ruedas acanaladas con una cuerda), los engranajes (que son ruedas dentadas) y los piñones (que encontramos más comúnmente en las bicicletas) estos, combinados, pueden dar origen a máquinas más complejas. Lo verás más adelante.
Pero por ahora, ¿Qué otra aplicación le damos a la rueda?
Para jalar un objeto verticalmente hacia arriba sin tener que cargarlo directamente, lo que da pie a hablar de la siguiente máquina simple que, en esta última diapositiva, estuvo muy mencionada, la polea, que en su funcionamiento incluye una rueda.
Así como un tornillo es un tipo de plano inclinado que gira sobre un eje, una polea es un tipo de rueda.

¿Cómo es que cambia la dirección de la fuerza aplicada? Es muy sencillo. Vuelve al ejemplo de tu caja. Si tú quisieras levantarla verticalmente y hacia arriba, tendrías que aplicar la fuerza hacia arriba. En este caso, con la polea, para levantar un objeto, en vez de aplicar una fuerza hacia arriba, la estarías aplicando hacia abajo, jalando la cuerda.
Una polea sencilla consiste en un eje donde gira una rueda libremente; el eje, a su vez, está suspendido, para soportar el peso de la carga. Una cuerda pasa por el canal de la rueda, sostiene la carga por un extremo y, por el otro, se aplica la fuerza.
Se jala la cuerda aplicando una fuerza hacia abajo, pero la carga sube. Tirar hacia abajo es más fácil que levantar algo, así nada más. Puedes usar tu propio peso para ayudarte. La gravedad está de tu parte.
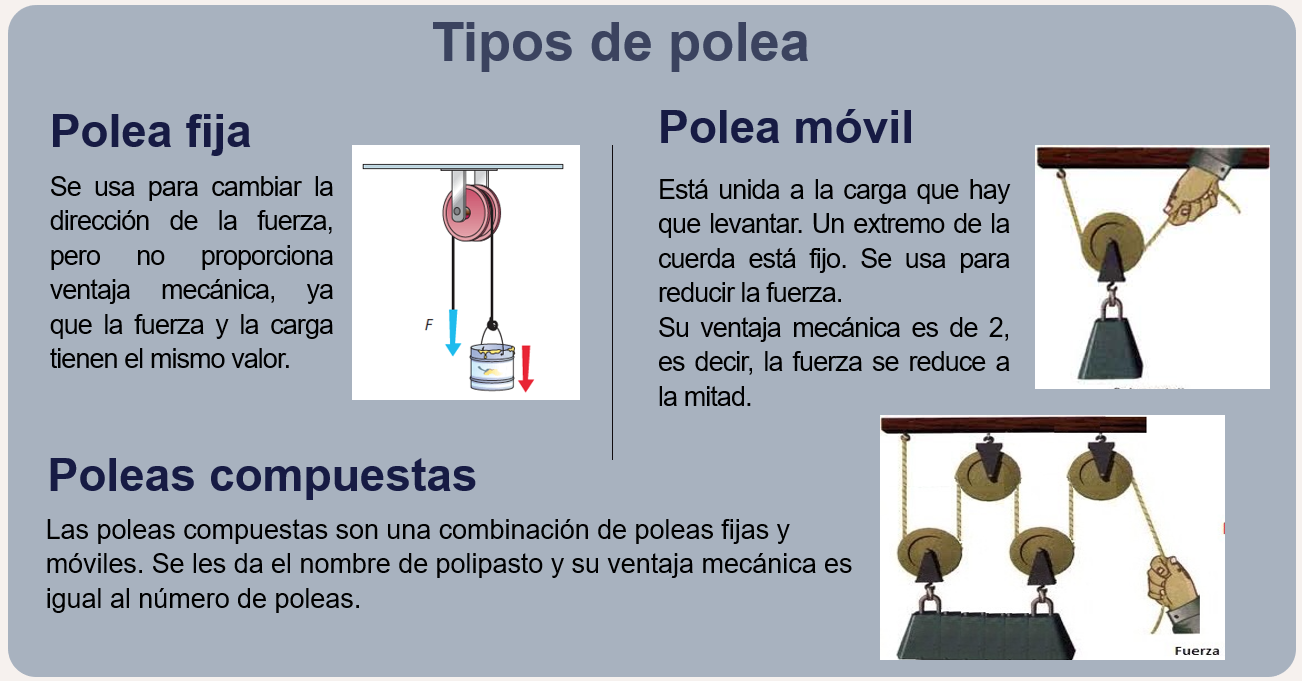
Las poleas pueden ser fijas, móviles y compuestas.
La polea simple no economiza fuerza. No, sólo sirve para cambiar la dirección y el sentido de la fuerza, pero la fuerza aplicada es la misma que la carga.
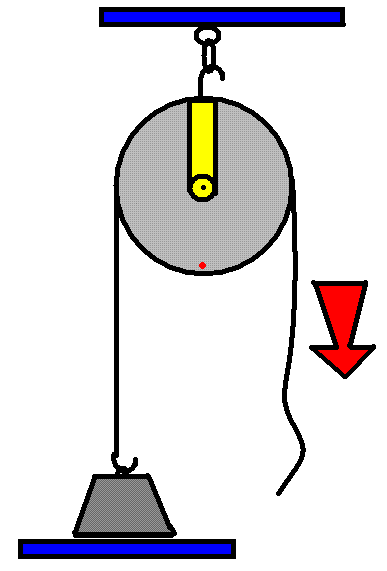
Un mástil de bandera tiene una polea fija. ¿Conoces otros ejemplos? ¿Podría ser el mecanismo que se usa en algunos cortineros o para levantar unas persianas, o para izar las velas de un velero? Correcto. En esos casos, la polea está en la parte superior sin desplazarse.
Una polea móvil es diferente.
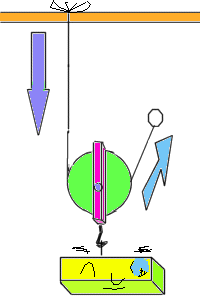
Está unida a la carga que hay que levantar. Un extremo de la cuerda está fijo, se usa para reducir la fuerza, su ventaja mecánica es de 2, es decir, la fuerza se reduce a la mitad.
Y hay también las poleas compuestas, que son una combinación de poleas fijas y móviles. Se les da el nombre de polipasto y su ventaja mecánica es igual al número de poleas, si tu levantas, con una polea fija, un objeto que pese 100 kilos, tendrás que aplicar 100 kilos de fuerza para levantarlo, pero si en vez de polea fija, es un polipasto de dos poleas, ¿Es como si esos 100 kilos de resistencia se redujeran a 50 kilos?
¿Y si tuvieras una polea más en ese polipasto? Sería la mitad de esos 50 kilos, es decir, ¡25 kilos! Por cada polea, ese peso se reduciría a la mitad, si tuvieras un polipasto de 10 poleas, ¡Tú solo podrías levantar toneladas!
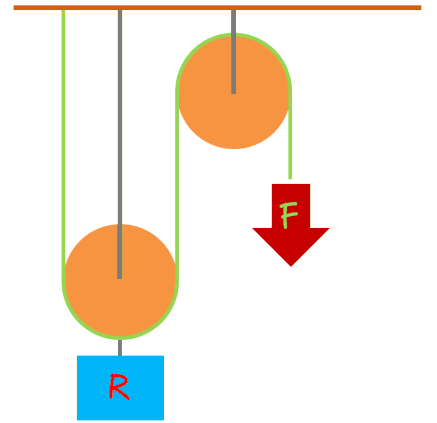
¡Es sorprendente cómo se reduce el esfuerzo con este sistema! Es por eso por lo que muchos motores tienen poleas. Las grúas de gran tamaño usan poleas para levantar cargas pesadas. Las grúas remolcadoras también, y las escaleras mecánicas. Hay poleas por todas partes.
Los polipastos son un gran ejemplo para empezar a hablar de las máquinas compuestas. ¿A qué te suena eso: “máquinas compuestas”?
MÁQUINAS COMPUESTAS |
Son máquinas con más piezas que las simples o, mejor dicho, que están hechas de varias máquinas simples trabajando de manera coordinada. Así es, los polipastos hacen que una resistencia se reduzca, por lo tanto, si se le aplica cualquier fuerza, esta se multiplica por el número de poleas, esto hace posible que se puedan emplear como multiplicadores de velocidad entre dos ejes. Aquí estás ante otra utilidad de las poleas: transmitir un movimiento giratorio de un eje a otro mediante correas, esta aplicación es de mucha utilidad para acoplar motores eléctricos a otras máquinas (compresores, taladros, ventiladores, generadores eléctricos, sierras).
Las máquinas compuestas son combinaciones de máquinas simples. El funcionamiento de cada una se va encadenando hasta conseguir un mecanismo más complejo, piensa, por ejemplo, en una polea que mueva una rueda que a su vez tiene un eje conectado a otra superficie que gira. El eje gira mucho más rápido que la rueda. Ahora imagínate que esa superficie del eje tiene un tornillo, ese tornillo serviría para taladrar una pared.
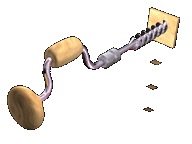
Y eso es un taladro! Ahora, revisa esta imagen. ¿Qué crees que sea?
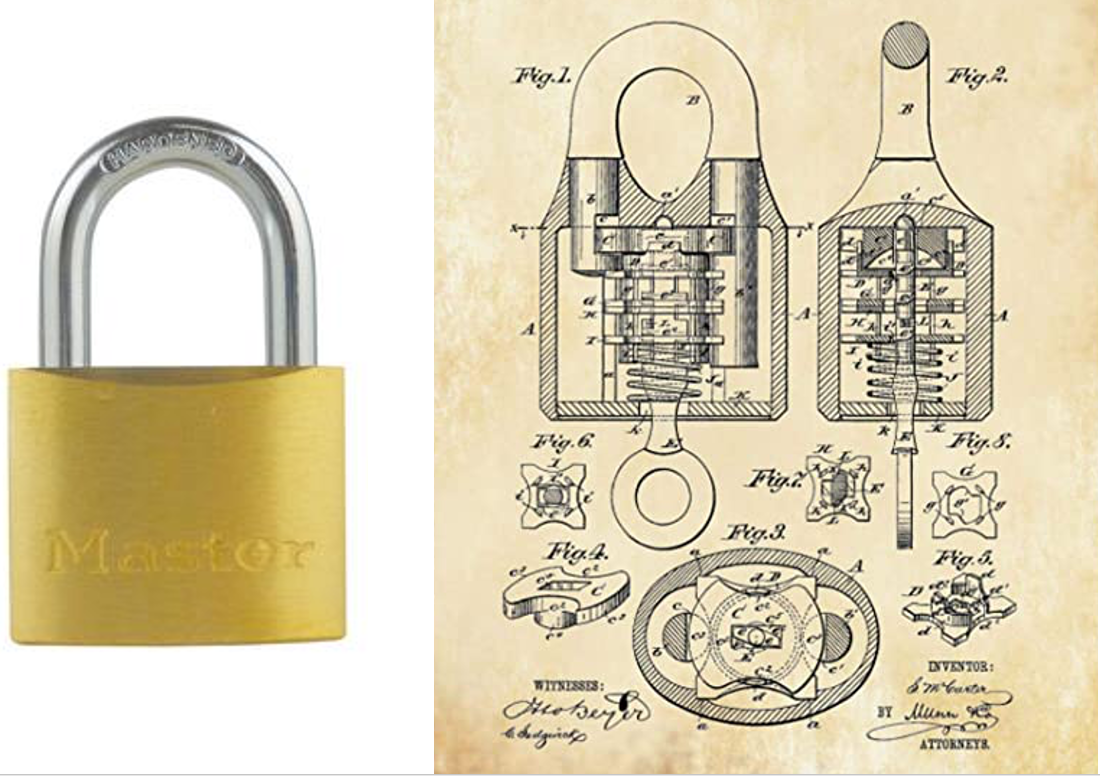
Es un candado. Si te fijas bien, hay ruedas, poleas, ejes, tornillos y hasta cuñas, y por supuesto, engranajes.
¿Qué tipo de máquina simple es un engranaje? El engranaje es una rueda dentada. Los engranajes están unidos a ejes.

Hacen que un objeto se mueva más rápidamente o más lentamente, necesitando más o menos fuerza para moverlo. Un engranaje grande se mueve más lentamente que uno pequeño.
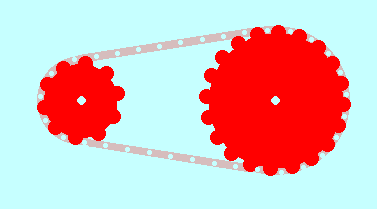
Y como imaginarás, al igual que las poleas, los engranajes pueden combinarse con otras máquinas simples.

Vas a jugar a identificar máquinas simples dentro de una máquina compuesta.
Observarás una imagen de una máquina compuesta. En una columna, anotarás qué máquinas simples logras identificar.
Primera imagen:

Esa es una carretilla. Puedes observar, en primer lugar, que tiene un eje con ruedas, con un movimiento de palanca. Tienes una carretilla que es una combinación de palanca con eje y ruedas.
Siguiente imagen:

Es un abrelatas. Tiene una cuña, que es con la que se perfora la lata y la pieza por donde se agarra y la manera en la que se clava en la lata, pues es una palanca. ¿Ya que la “clavaste” en la lata, cómo le das la vuelta para abrirla? Pues con un engranaje. Realmente, un abrelatas es una máquina compuesta.
Siguiente imagen:
|
|
Es una bicicleta, tiene ruedas, con sus respectivos ejes. ¿Qué dices de la cadena? ¿Sería una especie de polea? ¿Es una rueda que gira con una cuerda o, en este caso, con una cadena? Esa rueda es dentada, o sea que, sería un engranaje, esa pieza, formada de varios engranajes de varios tamaños, que sirve para cambiar las velocidades, se llama “piñón” ¿Te habías dado cuenta de lo compleja que es una bicicleta?
Observa ahora la siguiente imagen.
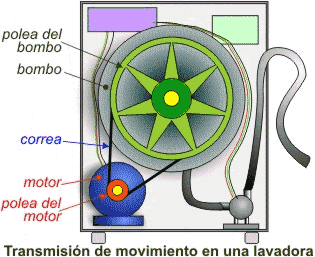
Es el mecanismo del interior de una lavadora. Fíjate muy bien, evidentemente hay una rueda que hace girar el contenedor donde se pone la ropa y, hay una polea, conectada al “motor” y si hay un motor, sabrás que hay poleas y engranajes.
¿Te das cuenta? Hay máquinas simples por todas partes, ahora ya sabes que, con las máquinas simples, tienes muchas opciones para mover o levantar objetos pesados.
Hoy recordaste qué son las máquinas simples y desde cuándo en la historia están presentes en la vida cotidiana. Observaste el caso de la invención de la rueda, hace aproximadamente 7000 años. Y los distintos usos que se le han dado, así como algunas de sus diversas aplicaciones. Que a su vez dan pie a otras máquinas simples, como el torno, el eje con ruedas y la polea.
Viste que existen distintos tipos de polea fija y movible, y que cuando encuentras varias juntas, se les llama “polipasto” a mayor número de poleas en el polipasto, menor será la fuerza requerida para levantar un objeto pesado.
Luego revisaste el concepto de “máquina compuesta o compleja” que son combinaciones muy eficientes de máquinas simples trabajando de manera coordinada.
Y también pudiste “descomponer” algunas máquinas compuestas en sus componentes: diversas máquinas simples.
El Reto de Hoy:
Comparte con un familiar la importancia de la fuerza en el uso de las máquinas simples, explícale como funciona.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Japón durante la Edad Media
Aprendizaje esperado: Identifica algunos rasgos de las culturas de Asia del siglo V al XV y sus aportaciones al mundo.
Énfasis: India, China y Japón del siglo V al XV.
¿Qué vamos a aprender?
Identificaras algunos rasgos de las culturas de Asia (India, China y Japón) del siglo V al XV y sus aportaciones al mundo.
Continuarás tu travesía histórica por el Lejano Oriente, solo que en esta ocasión te adentrarás en la historia de la extraordinaria cultura del Japón, el país del sol naciente.
Aprenderás sobre los orígenes de ese imperio, es decir, conocerás la historia de Japón durante los siglos V al XV, los siglos que duró la Edad Media en Europa. Conocerás lo que sucedió en Japón mientras en Europa se desarrollaba el feudalismo.
Debes tener listos tu lápiz o pluma, cuaderno y, por supuesto, tu libro de Historia en la página 98
https://libros.conaliteg.gob.mx/20/P6HIA.htm?#page/98

¿Qué hacemos?
Para comenzar considera que en un principio la civilización de Japón estuvo fuertemente influida por la cultura de China, pero con el paso de los siglos los japoneses supieron desarrollar una cultura muy propia y original.
Esa influencia de China en Japón se debió, en buena media, a la cercanía geográfica que existe entre ambos países.
Un ejemplo de esa influencia de China en Japón es el kimono, se trata de una prenda tradicional china que los japoneses adoptaron y transformaron de acuerdo a sus propios gustos y necesidades, los japoneses no solo tomaron de los chinos sus formas de vestir sino también otras cosas.
Los japoneses también retomaron de la civilización China su escritura, la religión budista, filosofías como el confucianismo y, sobre todo, la forma de gobierno imperial. Entonces, lo interesante será conocer el modo cómo los japoneses adoptaron y transformaron esta influencia de China hasta dar origen a una cultura propia y muy original.
Observa el siguiente video que trata de una entrevista a un especialista de El Colegio de México que hablará sobre las filosofías y las religiones chinas, algunas de las cuales fueron retomadas por los japoneses durante los siglos V al XV.

- Video. Cápsula con el especialista.
Ahora ya sabes que el confucianismo, el taoísmo y el budismo fueron filosofías-religiones que se desarrollaron en China durante los siglos V al XV.
Recuerda que el taoísmo enfatiza la armonía con el tao, que es la unidad absoluta y mutable que conforma la realidad suprema de todas cosas. El budismo busca superar el sufrimiento causado por el deseo y la ignorancia. Y el confucianismo es una filosofía-religión que, entre otras cosas, planteaba la relación entre forma-idea, sujeto-objeto, conocimiento-acción.
Como verás en esta clase, tanto el budismo como el confucianismo fueron filosofías-religiones que los japoneses tomaron de los chinos y las utilizaron para darle forma a su propio imperio.
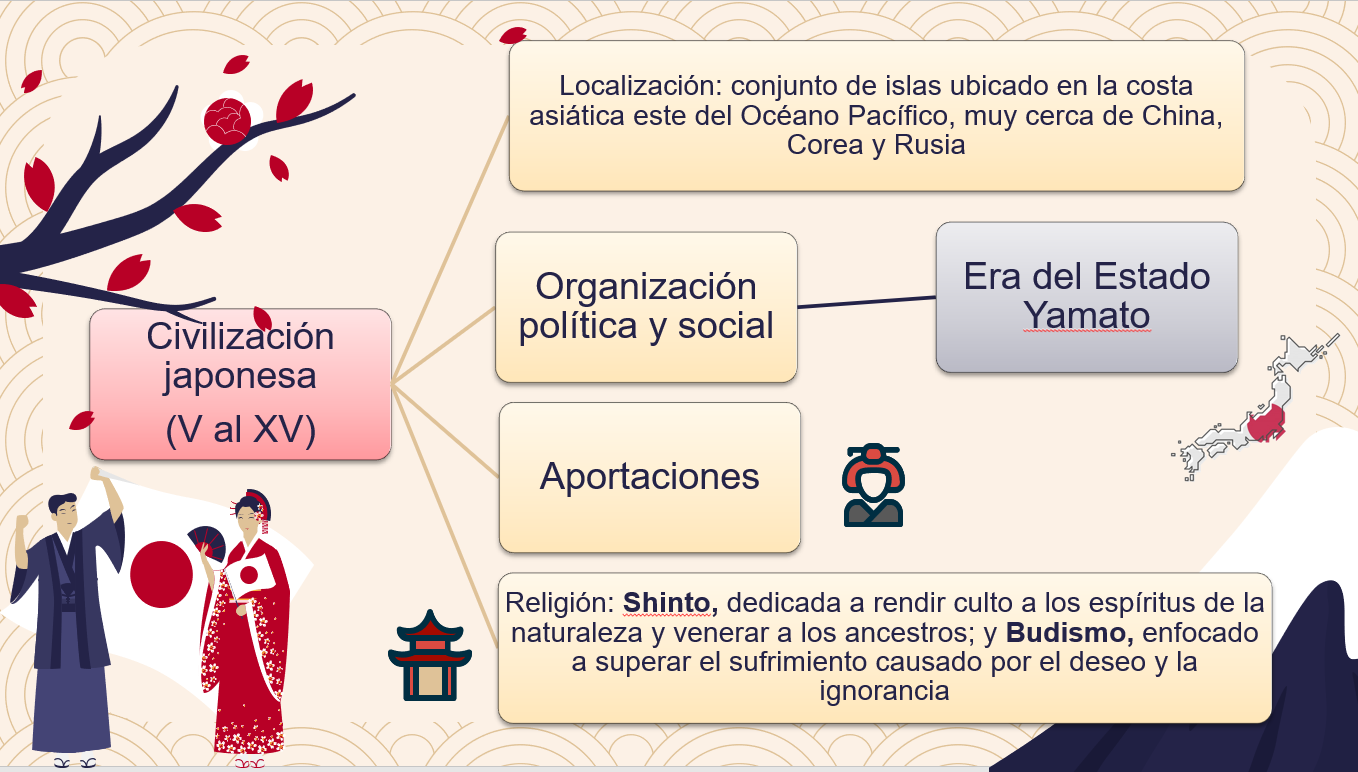
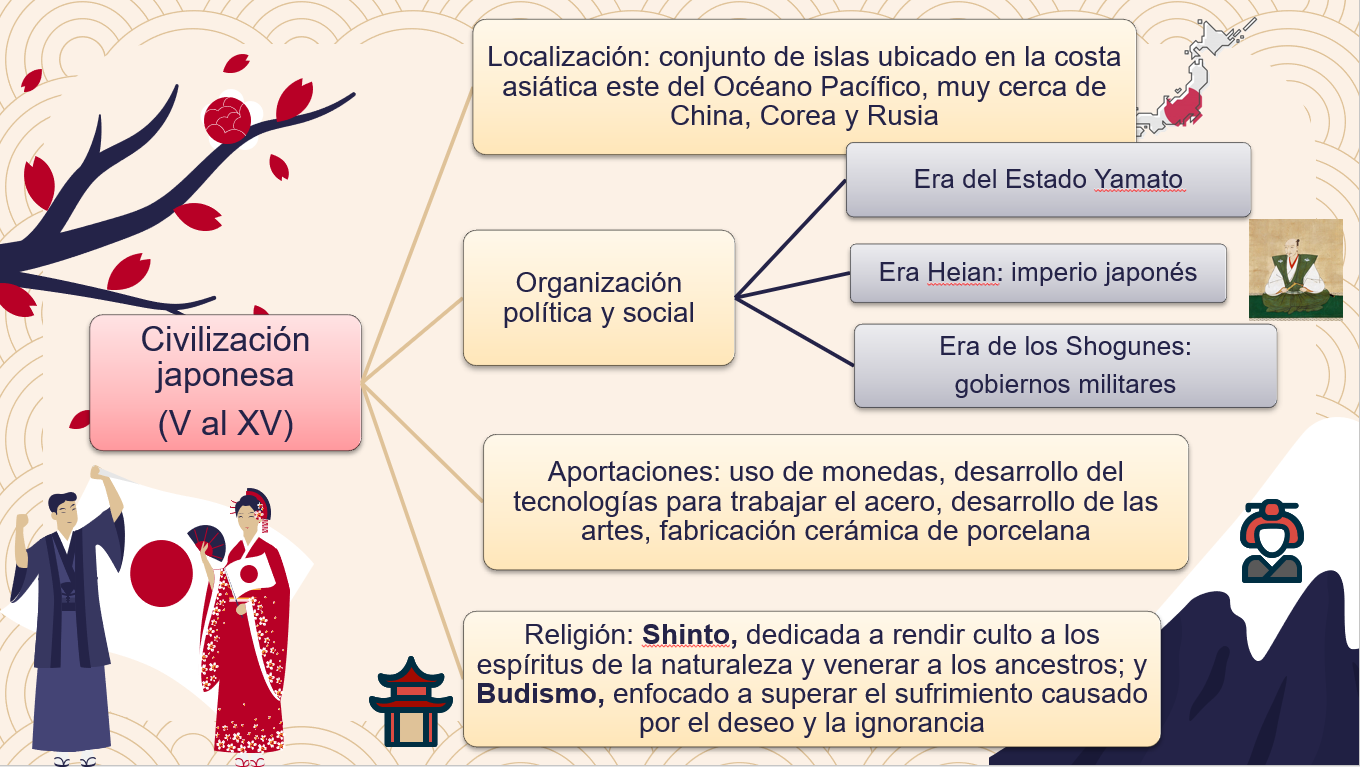
Elabora un cuadro sinóptico, en el que anotes los aspectos más relevantes de la civilización japonesa, tales como: Localización, Organización política y social, Aportaciones, Religión, y Expresiones culturales y artísticas.
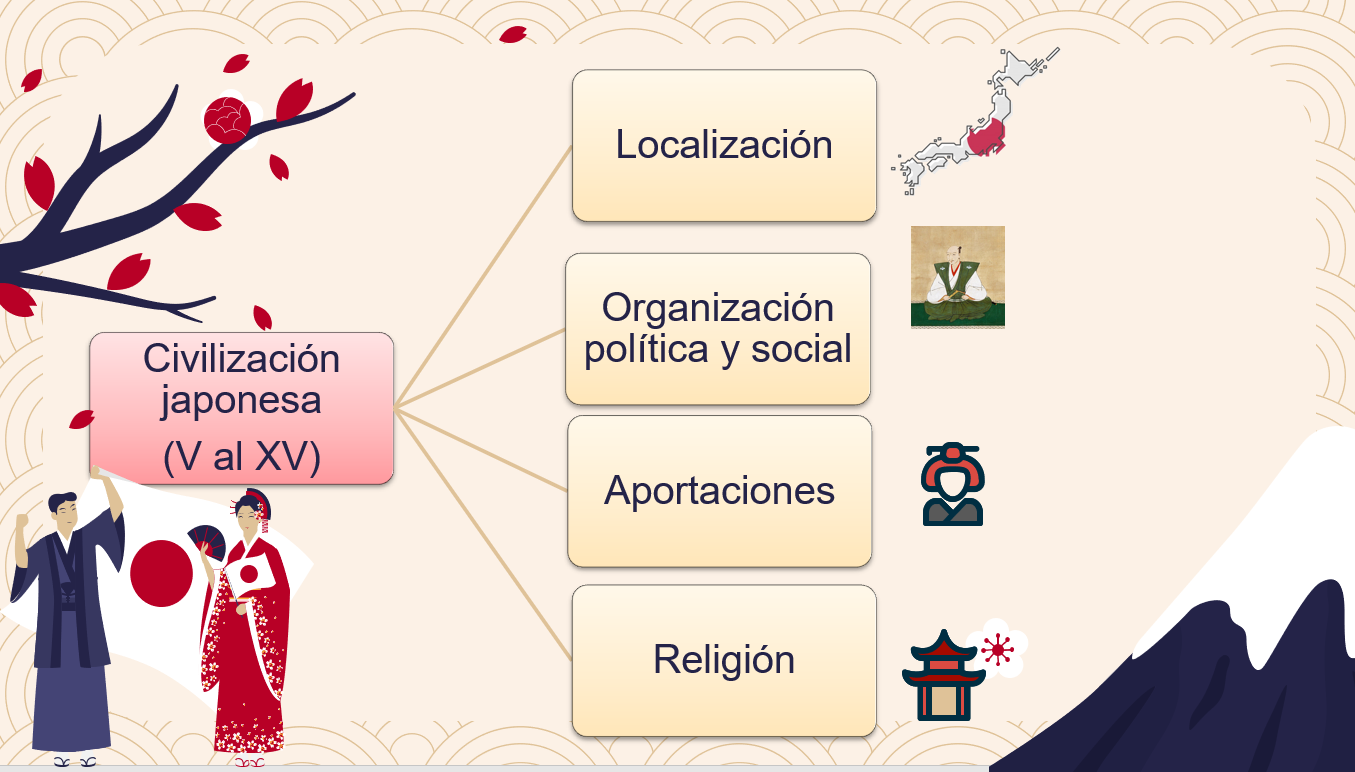
Localización. Japón está ubicado en la costa asiática este del océano Pacífico, muy cerca de las costas de Rusia, China y Corea. La característica principal de Japón es que es un archipiélago, es decir un conjunto de más de 6 mil islas. Las islas más grandes que conforman Japón son 4: Hokkaido, Honshu, Kyushu y Shikoku.
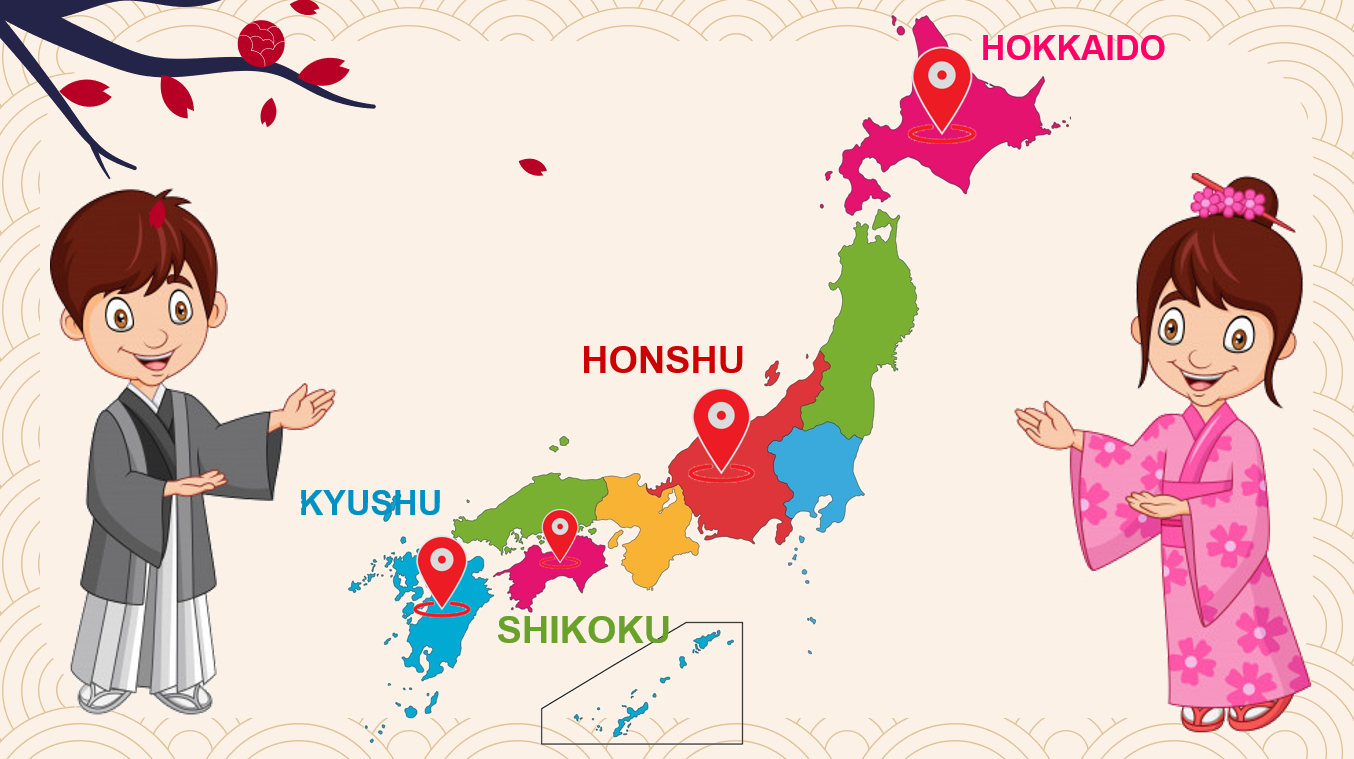
Precisamente por ser un conjunto de islas la historia de Japón es muy peculiar. Por un lado, es un país que logró mantenerse a salvo de las invasiones de los pueblos nómadas de Manchuria y lo que hoy es Mongolia que atacaron a imperios como el chino, pero, por otro, es un país que se mantuvo por mucho tiempo aislado del mundo.
Esas islas que conforman Japón son en realidad montañas, cuyas bases están sumergidas en el océano. Esto provoca que en Japón haya muchos volcanes, temblores y olas gigantescas que a veces inundan la tierra.
Fue en este complicado espacio isleño que surgió la civilización japonesa, gracias al paulatino desarrollo de la agricultura.
Puedes comenzar a llenar tu cuadro sinóptico anotando lo siguiente:
“Civilización japonesa. Localización: Conjunto de islas ubicado en la costa asiática este del Océano Pacífico, muy cerca de China, Corea y Rusia”
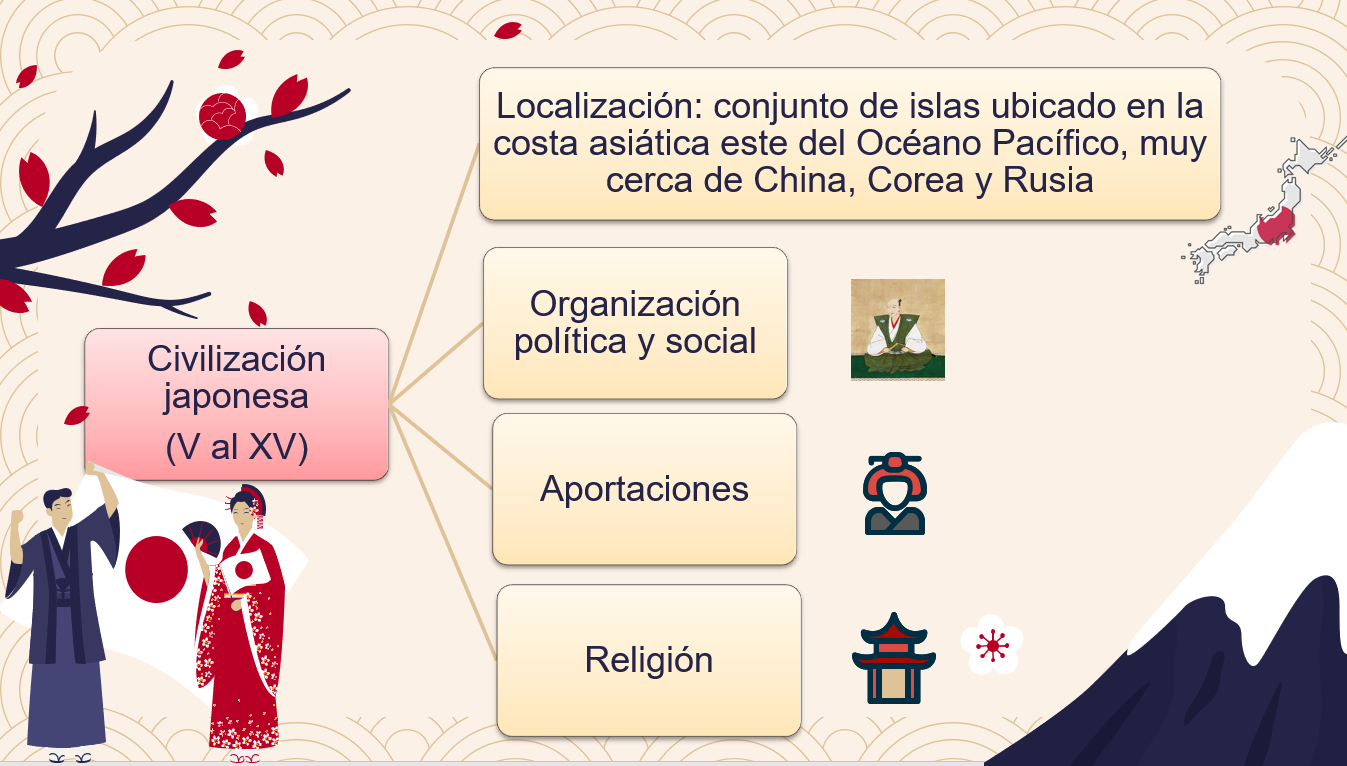
Prosigue. A partir del siglo IV, es decir por ahí del año 300 d. C., puede decirse que comenzó la historia de la conformación de la civilización japonesa. A partir de ese siglo se hace evidente la paulatina conformación de una organización política cada vez más compleja, el crecimiento de una sociedad japonesa cada vez más estratificada, y el desarrollo de sistemas de escritura y de creencias cada vez más acabados. Para entender mejor este proceso, los historiadores hablan de tres grandes etapas en la historia de la civilización japonesa durante los siglos IV al XV.
La etapa del Estado Yamato (IV – VII)
La era Heian (VIII – XI)
La era de los Shogunes (XII – XV)
Esto hay que anotarlo en tu cuadro sinóptico, en el apartado correspondiente a “Organización política y social”.
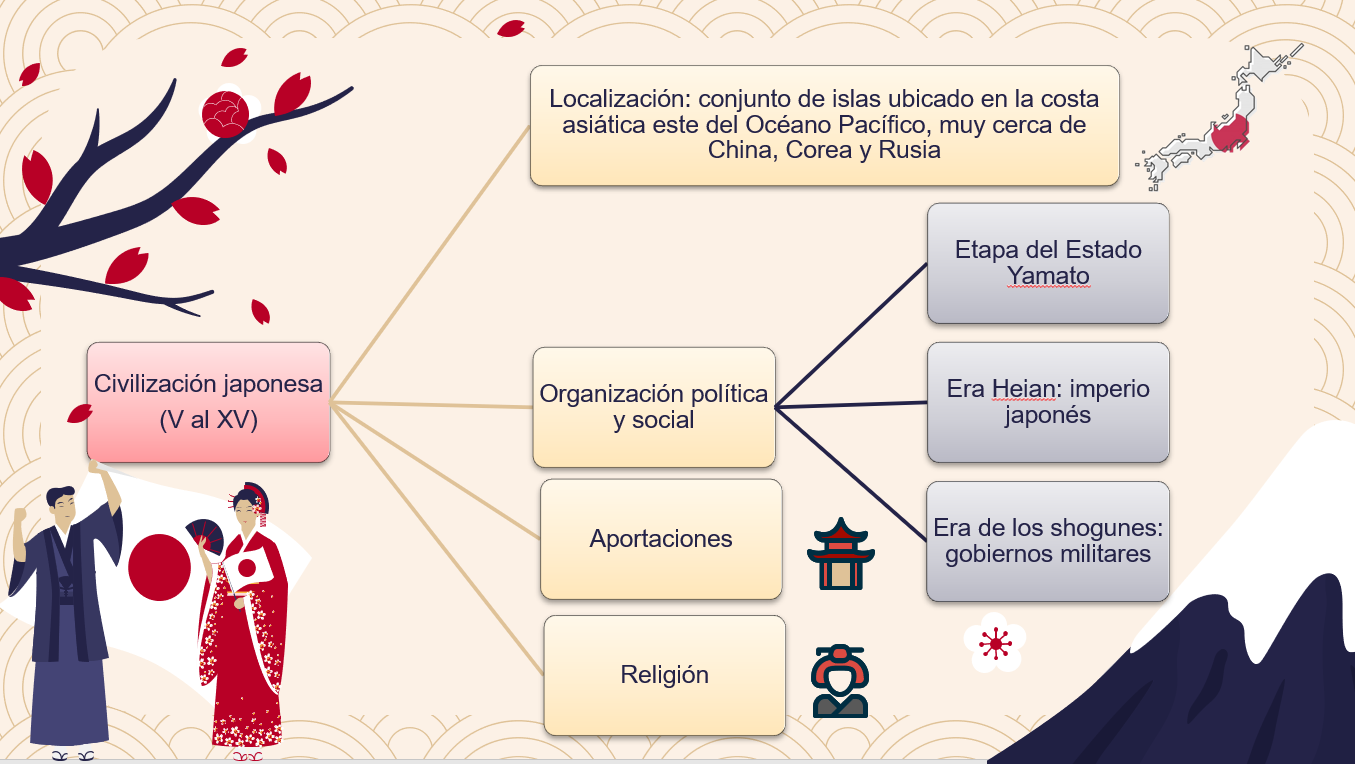
Revisa ahora cuáles fueron las principales características de cada una de estas etapas.
La etapa del Estado Yamato es una parte de la historia japonesa que se desarrolla entre los siglos IV al VII durante estos siglos, la agricultura, sobre todo el cultivo de arroz, se consolidó, sobre todo en la parte sur del archipiélago. Gracias al excedente agrícola, el Estado Yamato comenzó a crecer y crecer: De ser un pequeño reino pasó a convertirse en un Estado que se expandía paulatinamente por las otras islas de Japón, teniendo un mayor control político y económico sobre sus pobladores. Pruebas de este desarrollo y expansión del Estado Yamato fueron las famosas tumbas o Kofun.

Se trata de grandes túmulos de tierra encontrados alrededor de los núcleos habitados de las llanuras del centro de Japón que presumiblemente se destinaron a rituales funerarios de las élites dominantes. La edificación de estos túmulos gigantescos resultaba tan extremadamente costosa que constituye una prueba de la existencia de un Estado bastante consolidado que era capaz de destinar enormes recursos económicos para su construcción. Estas tumbas las construían los campesinos o los miembros de los estratos más bajos del Estado Yamato, otra característica del Estado Yamato es que su sociedad se volvió cada vez más compleja y estratificada, quedando conformada por tres estratos principales:
- Los uji: Clanes familiares que constituían la clase dirigente del Estado.
- Los be: Servidores de los uji que se agrupaban y distinguían según su actividad laboral, campesinos, pescadores, ceramistas y fabricantes de arcos.
- Los yatsuko: Funcionarios que pertenecían al Estado y no disfrutaban de libertad personal.
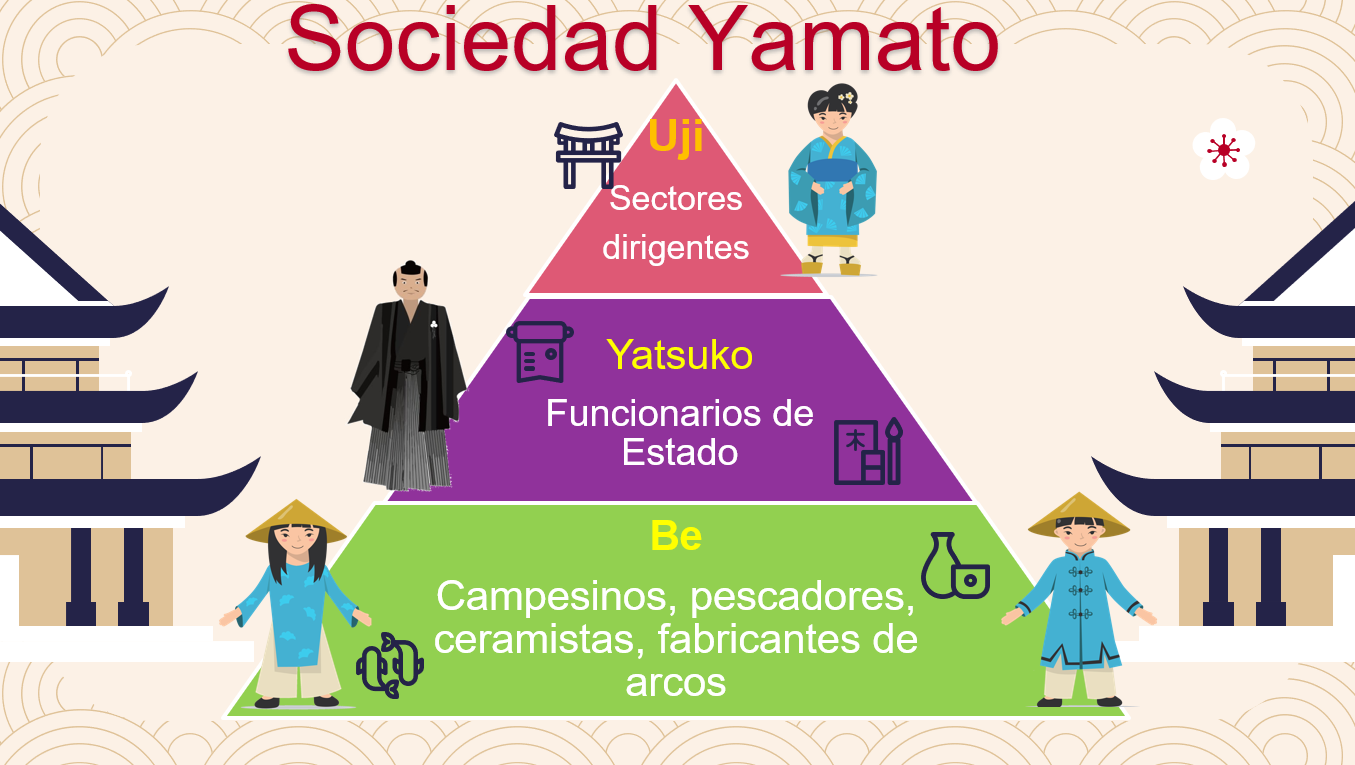
La estratificación de las sociedades es un aspecto que los historiadores toman muy en cuenta a la hora de hablar de las civilizaciones del pasado, ya que es una muestra clara del crecimiento de su población, de su paulatina especialización productiva y de una mayor complejidad económica, social y política. Esta es la razón de que siempre encuentres estas pirámides en todas las sociedades del pasado.
Otro rasgo de esta sociedad cada vez más compleja del Estado Yamato es que se basaba en una red dinámica de intercambio de favores, sobre todo de intercambio de favores entre los clanes dirigentes que, de este modo, afianzaban su poder. Un ejemplo de este intercambio de favores pueden ser los matrimonios.
Los matrimonios entre clanes dirigentes uji eran muy frecuentes e importantes, ya que gracias a ellos accedían a ciertos privilegios, obtenían cargos en el Estado Yamato, y aseguraban su poder y su linaje.

Al principio de la clase mencionaste que fue durante los primeros siglos de la Edad Media en Japón que se dieron los intercambios entre China y Japón, supongo que te referías a esta etapa del Estado Yamato.
Durante la etapa del Estado Yamato los contactos con el continente asiático fueron muy intensos y tuvieron un papel determinante en la evolución tecnológica, económica, social, política, cultural y religiosa de Japón.
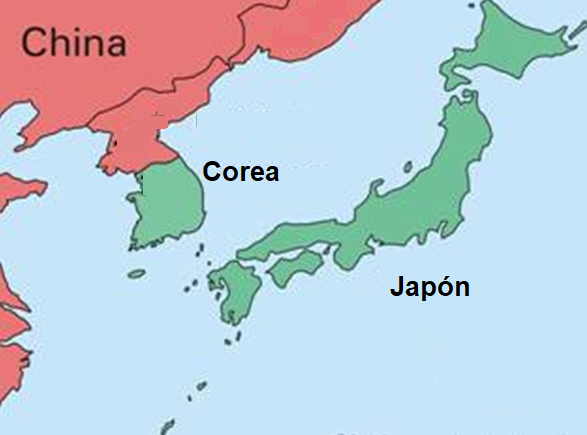
Los clanes dirigentes del Estado Yamato fomentaron, sobre todo, los intercambios con China y Corea, lo que permitió la entrada a Japón del budismo.

Muchos miembros de los clanes dirigentes adoptaron el budismo como su religión, lo que supuso una fuerte competencia con la religión que ya existía en Japón desde mucho tiempo atrás: El shinto o sintoísmo, religión dedicada a rendir culto a los espíritus de la naturaleza y venerar a los ancestros.

Debes anotar esta información en tu cuadro sinóptico, en el apartado correspondiente a la “Religión”. Puedes escribir por ejemplo:
“Religión: Shinto, dedicada a rendir culto a los espíritus de la naturaleza y venerar a los ancestros; y Budismo, enfocado a superar el sufrimiento causado por el deseo y la ignorancia”.
Habría que agregar que los japoneses no solo adoptaron de los chinos la religión budista, sino que también es muy notable la influencia de China en la escritura, la arquitectura y el modelo político del imperio chino que quisieron adoptar, lo que lleva a hablar de la segunda era en la historia de la civilización japonesa.
La Era Heian. Ante el inminente declive del Estado Yamato durante el siglo VII, se intentó dar mayor poder y realce a una nueva figura gobernante: el emperador, lo que trajo cambios importantes en la estructura política de la sociedad japonesa.
Siguiendo el modelo de China, los japoneses se esforzaron por establecer un imperio centralizado y fuerte, capaz de controlar a una mayor población y un mayor territorio. El primer emperador de esta nueva era del Imperio japonés se considera que fue Kanmu Tenno, Gracias a sus excelentes vías de comunicación por tierra, mar y ríos, Heian fue la capital del Imperio durante casi 1000 años, aproximadamente del 768 hasta 1868

Por eso esta segunda etapa de la historia japonesa recibe el nombre de Era Heian: Heian por ser el nombre de la capital del nuevo imperio japonés que se intentó consolidar entre los siglos VII y XI.

Ahora bien, al igual que los chinos, los japoneses consideraron a su emperador “Hijo del cielo y el padre de la Tierra”, al menos así quedó establecido en la primera constitución de la historia japonesa, redactada hacia el año 604 por el regente, el príncipe Shotoku.
El regente Shotoku era uno de los tantos ministros que gobernaban el Imperio, porque aquí hay que entender algo: aunque el emperador era la máxima autoridad del Imperio, el padre de todos sus súbditos siempre estaba acompañado y asesorado por una aristocracia de la que salían los principales funcionarios del imperio, es decir, los regentes y gobernantes encargados de las funciones cotidianas del Estado.

Un ejemplo de esta aristocracia que ejercía las funciones de gobierno del Imperio fue el famoso clan Fujiwara, un clan de la aristocracia japonesa que comenzó a tomar el control del imperio gracias a los matrimonios que establecía entre sus hijas y los hijos del emperador.

Aun cuando era muy importante, el emperador era más una autoridad simbólica, ritual, que un gobernante real del imperio y es que los miembros de la aristocracia japonesa, como el clan Fujiwara, no solo llegaron a ser funcionarios del Estado, sino también los explotadores de las tierras, lo que les otorgaba mucho poder.
Eran explotadores, porque el único dueño de la tierra era el Estado imperial y éste le daba autorización a los miembros de la aristocracia para que la explotaran, es decir, la cultivaran con la ayuda de siervos o campesinos. Como puedes observar fue una sociedad sumamente compleja y estratificada. Y dentro de esta sociedad también existió un sector que cobró vital importancia durante la última etapa de historia japonesa, se trata de la clase guerrera del imperio.
Se trató de la clase guerrera, una élite militar, de la cual después salieron los famosos samuráis, de los que tanto has oído hablar en películas, comics y cuentos. Esta clase guerrera comenzó a conformarse desde el siglo VIII, cuando se le encomendó el mantenimiento de un Imperio japonés que, pese a todos los esfuerzos, estaba fragmentado geográficamente. En sus inicios, se trata de una clase guerrera formada por guerreros montados a caballo que procedían de las noblezas locales.

Eran guerreros muy habilidosos montando a caballo, que además tenían bastante pericia en la caza y el uso del arco. Los más famosos llegaron a ocupar puestos en el Estado y a poseer territorios. Con el tiempo estos guerreros y los señores terratenientes para los que trabajaban adquirieron tanto poder en las distintas provincias del Imperio japonés que acabaron por protagonizar las grandes luchas por el control del territorio que marcaron el fin al periodo Heian y el inicio de una nueva era.
Sobre la era de los shogunes tu libro de texto explica que un shogun era jefe de los ejércitos, que comenzó a imponerse y despojar al emperador de su poder político hasta establecer una “dictadura militar”. Este shogun no solo concentraba la autoridad política y militar, sino que, además, era dueño de las tierras cultivables que repartía entre señores feudales a cambio de una renta.

La era de los shogunes recibió este nombre porque se trató de un periodo de la historia japonesa en el que el poder político, económico y social recayó en jefes militares que, a su vez, tenían bajo su control a señores terratenientes que se dividían la defensa y el control del territorio japonés, con la ayuda de los samuráis.
Este sistema se parece mucho al sistema feudal europeo, a este sistema de control político, militar y territorial se le conoce como feudalismo japonés porque funcionó bajo una lógica semejante al del vasallaje europeo: Un jefe político-militar máximo que otorga tierras a otros señores feudales, a cambio de lealtad y servicios, para que éstos se encarguen de proteger controlar y cultivar sus respectivos territorios con la ayuda de vasallos.
Esta era de shogunes inició por ahí del año 1192, después de la llamada guerra Genpei, y concluyó hasta 1868 cabe señalar, que, en el siglo XV, aproximadamente en el año 1467 en el que se originó un nuevo periodo histórico caracterizado por guerras permanentes. Durante la era de los shogunes se registró un avance considerable en las técnicas de explotación agrícola, se introdujeron nuevas variedades de arroz a Japón, se desarrollaron las artes, como el teatro, la poesía, la caligrafía, y se favoreció el intercambio comercial entre todos los territorios del archipiélago.
Gracias a este intercambio comercial, el uso de monedas de oro, plata y cobre se volvió cada vez más frecuente en Japón, hasta convertirse en uno de los grandes adelantos del periodo.



Puedes terminar tu cuadro anotando en “Aportaciones” de la civilización japonesa los siguiente:
“El uso de monedas, el desarrollo de las tecnologías para trabajar el acero, que se utilizaban en la fabricación de espadas (katanas), el desarrollo de las artes como la poesía, la música, el teatro y la fabricación cerámica de porcelana.”
El Reto de Hoy:
Concluye la elaboración de tu cuadro sinóptico, revísalo y complétalo, de ser necesario y preséntalo a algún familiar cercano, seguramente la cultura del Japón en la edad media, le parecerá muy interesante.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Partes de unas cantidad
Partes de unas cantidad
Aprendizaje esperado: Resuelve problemas que impliquen calcular una fracción de un número natural, usando la expresión “a/b de n”.
Énfasis: Relaciona el cálculo de n/m partes de una cantidad con la multiplicación y la división.
¿Qué vamos a aprender?
Aprenderás a resolver problemas que impliquen calcular una fracción de un número natural, usando la expresión “a/b de n”, para hacerlo relacionarás el cálculo de n/m partes de una cantidad con la multiplicación y división.
¿Qué hacemos?
Para iniciar es importante que reconozcas que aun en pleno 2021 existen muchas personas que no saben leer, ni escribir debido a que no tuvieron la oportunidad de acudir a la escuela por diversas circunstancias.
Por ejemplo, los abuelitos de la maestra Laura, nacieron en 1913 y 1914 dice que su abuelito Adolfo no sabía leer, ni escribir y se le dificultaban las operaciones matemáticas, sin embargo, su abuelita Manuela, sí sabía y ella lo ayudaba. Los recursos económicos que cada uno tenía cuando fueron niños, marcaron la diferencia que había entre ellos.
Los padres de la abuelita si tenían dinero para enviarla a una de las pocas escuelas que había en ese momento o para pagar alguna persona que les pudiera enseñar y el abuelito no, él era huérfano y tenía que trabajar.
Los abuelitos nacieron hace más de 100 años, quizá ya casi no hay personas analfabetas.
|
|
|
|
¿Habrá gente más joven que la abuelita de la maestra Laura, que no sepa leer y escribir en la actualidad?
Aunque las circunstancias eran diferentes hasta no hace muchos años, observa lo que pasa actualmente. Para ello visita la página CUENTAME del INEGI donde existe información para niños. Hay información que se ha recabado en los censos, el último fue realizado en el 2020 identifica la información que tiene sobre el analfabetismo.
Aunque en el país la educación básica (preescolar, primaria y secundaria) cada vez llega a más lugares, muchos jóvenes, por diversas razones, no asisten a la escuela y por lo tanto, algunos de ellos no saben leer ni escribir.
Analfabeta(o): Es la persona de 15 o más años de edad que no sabe leer ni escribir un recado.
En México, durante los últimos 50 años, el porcentaje de personas analfabetas de 15 y más años bajó de 25.8 % en 1970 a 4.7 % en 2020 lo que equivale a 4,456,431 personas que no saben leer ni escribir.
De las personas que no saben leer ni escribir actualmente según esta información, ¿De qué edad estimas que sean en su mayoría?
Observa la siguiente información que hay en esta página.

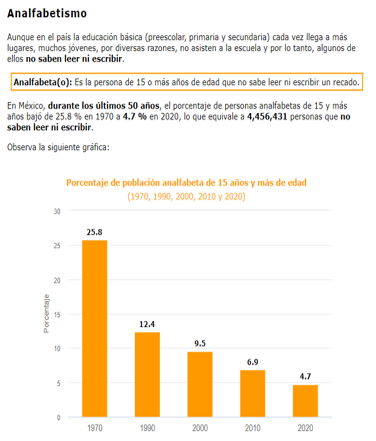
Por sexo. De acuerdo con el Censo de Población y Vivienda 2020 cuatro de cada 100 hombres y seis de cada 100 mujeres de 15 años y más no saben leer ni escribir.
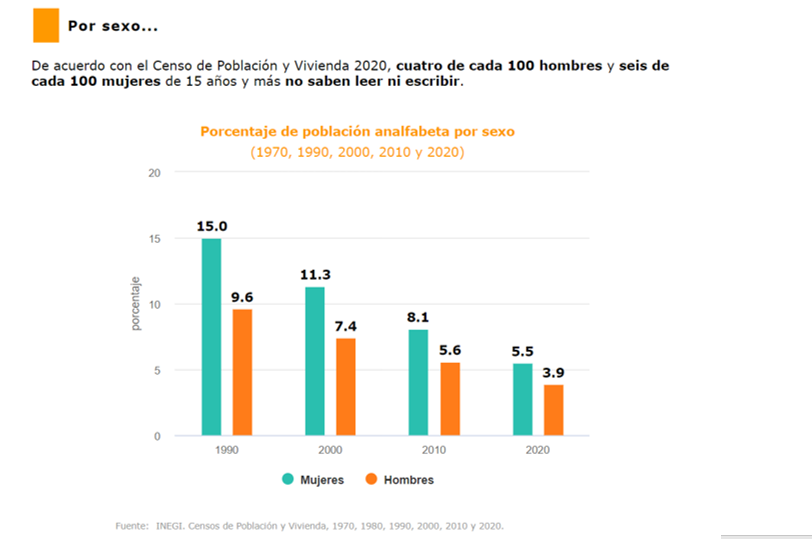
Hay quien piensa que sólo habría personas de mayor edad que no supieran leer ni escribir, pero según esta información, también hay jóvenes de 15 años que no saben leer ni escribir, existen diversas circunstancias que provocan esta situación.
Analiza desde las matemáticas esta información, decir 4 de cada 100 hombres de 15 años y más, no saben leer ni escribir es una razón, de acuerdo con lo que has aprendido en otros programas.
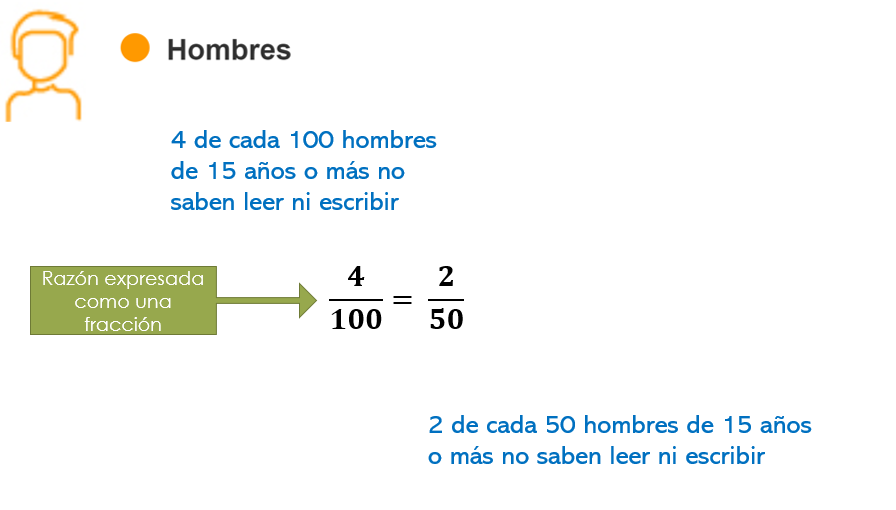
Recuerda que se puede expresar como una fracción, esto es cuatro centésimos. Además, si se reduce observa que es equivalente a la fracción dos cincuentavos, lo cual se interpreta como 2 de cada cincuenta hombres de15 años y más, no saben leer ni escribir.
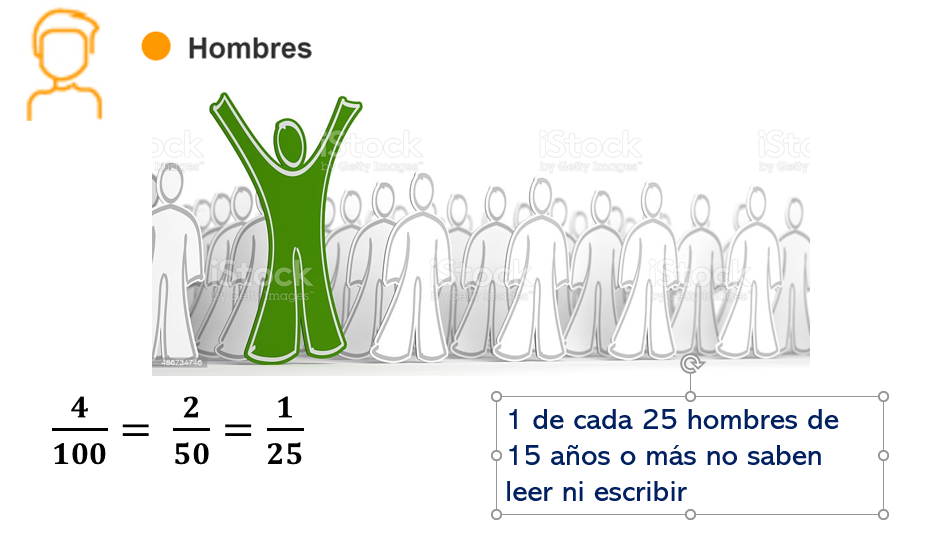
Se puede reducir aún más si le sacas mitad a la fracción dos cincuentavos, entonces queda un veinticincoavo.
¿Qué interpretación tendría en la situación que se está investigando?
¿Será uno de cada veinticinco hombres?
Significaría que de un grupo de veinticinco hombres de 15 años o más, uno de ellos no sabe leer ni escribir.
Increíble, pero cierto, por cada grupo de 25 hombres, uno de ellos no sabe leer y escribir, entonces, ¿Cuántos hombres de 15 años o más no saben leer ni escribir en total en México?
Habría que seguir investigando algunos datos más, por ejemplo, cuántos hombres de 15 años y más hay en el país y de ahí podrías calcularlo aplicando la razón o fracción que obtuviste.
Observa este dato: la población de hombres mayores de 15 años y más es de 45 millones, 252 mil, 363 esa cantidad demuestra que si son muchos los hombres que por alguna razón no saben leer ni escribir.
Hoy conocerás algunas estrategias que te permitirán hacer cálculos para saber cuántos hombres de 15 años y más están en esa condición, de acuerdo con el censo 2020
Así que es momento de empezar con el libro de texto. Localza la página 117 Desafío 60, Partes de una cantidad.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/117

Como lo menciona la consigna, analiza la información que presentan los problemas que integran este desafío.
Problema 1. En un grupo de 36 alumnos, un tercio del total son menores de 10 años.
¿Cuántos tienen 10 o más años?
¿Qué parte del grupo tiene 10 o más años?

Considera la información que presenta el problema e imagina a un grupo de 36 personas en las que hay personas menores de 10 años y mayores que 10 años, de acuerdo con lo que indica el problema. ¿Qué observan? ¿Qué relaciones encuentran entre los datos?
Dice un tercio del total son menores de 10 años quiere decir que 1 de cada 3 estudiantes son menores de 10 años.
Esa es la razón que corresponde a la fracción un tercio, en esta situación. ¿Cómo podrías representar esta información gráficamente?

De esta manera puedes identificar que son 4 estudiantes de 12 menores de 10 años y así continuarías.
A partir de la representación gráfica de la razón: 1 de cada 3 estudiantes son menores de 10 años, encuentras diferentes pares de grupos de estudiantes que corresponden con esa razón y que también representan la fracción, un tercio.
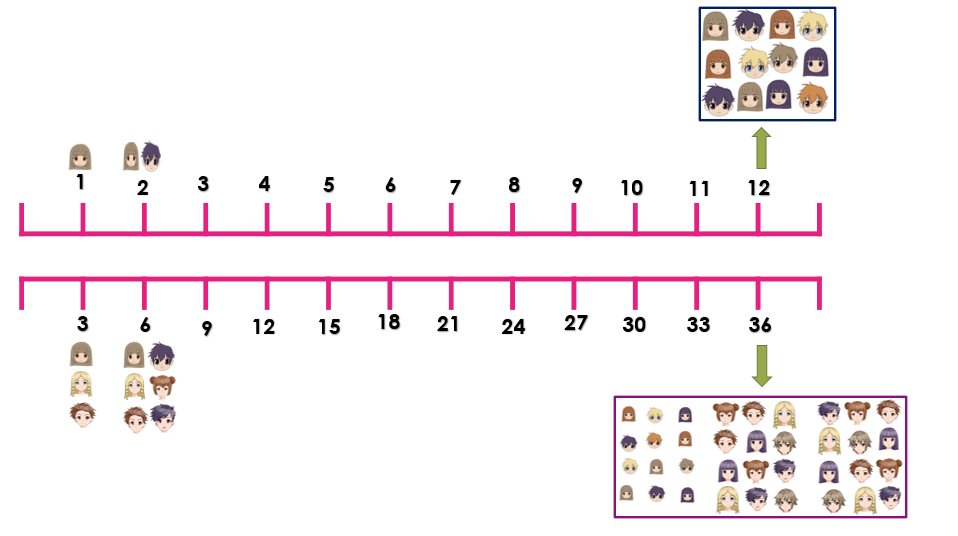
Aplicando la propuesta, aumentó de manera proporcional y se llegó a 12 estudiantes de 36 son menores de 10 años.
Como puedes observar, se fueron aumentando las cantidades de forma proporcional hasta que se encontró el 36 que es el total de estudiantes del grupo que menciona el problema.
Entonces, ya sabes que 12 alumnos de 36 son menores de 10 años. Ahora, ¿Cómo usar esta información para saber cuántos estudiantes tienen 10 o más años?
Se puede saber restando 12 a 36: 36 – 12 = 24
Observa, treinta y seis menos doce es igual a veinticuatro. Eso significa que veinticuatro estudiantes tienen 10 o más años en ese grupo de treinta y seis estudiantes.
Esta es otra manera de obtener el resultado, cada quien va encontrando distintas estrategias y formas para llegar al resultado.
Conoce otra estrategia más, observa, qué sucede si se interpreta un tercio de 36 estudiantes son menores de 10 años como la división de treinta y seis estudiantes entre tres.

Así se obtienen tres grupos de 12 estudiantes, uno de cuales es el de los estudiantes menores de 12 años, y los otros dos grupos de 12 estudiantes tienen 10 años o más.
Observa que se encontraron las dos cantidades que se necesitan para dar respuesta a la pregunta; un tercio que son 12 niños menores de 10 años y 24 de 36 estudiantes tienen 10 o más años.

A través de la división también se puede llegar a la respuesta de la pregunta que se plantea en el libro, ¿Cuántos estudiantes tienen 10 o más años?
Podrías escribirla como fracción 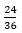
De esta manera, se pueden buscar fracciones equivalentes hasta llegar a su mínima expresión, es decir, donde ya no se puedan reducir más. Así que empieza por dividir a la mitad o entre 2
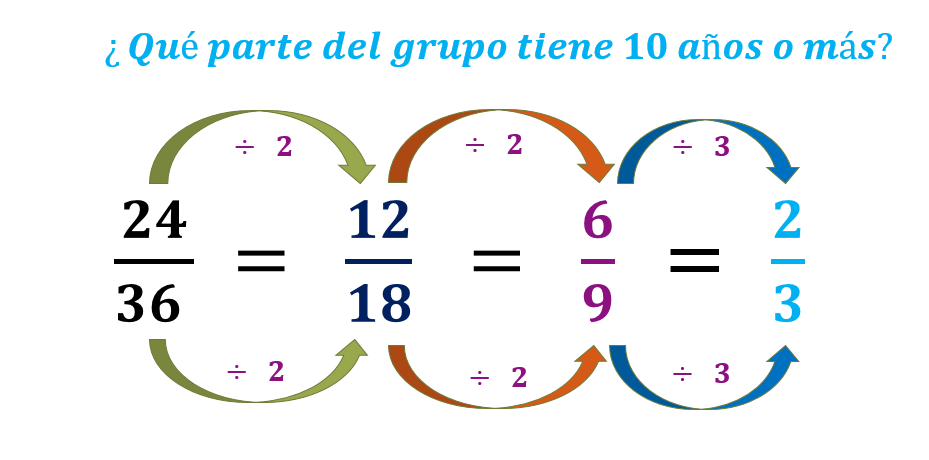
Se obtiene la mitad de 24 y 36 y es 12 de 18 también puedes sacar mitad y queda 6 de 9 y ya no se puede sacar mitad.
Piensa en un número que divida exactamente al 6 y al 9 y es el 3, 6 entre 3 = 2 y 9 entre 3 = 3 por lo tanto, 2 tercios es la parte del grupo que son estudiantes de 10 años o más.
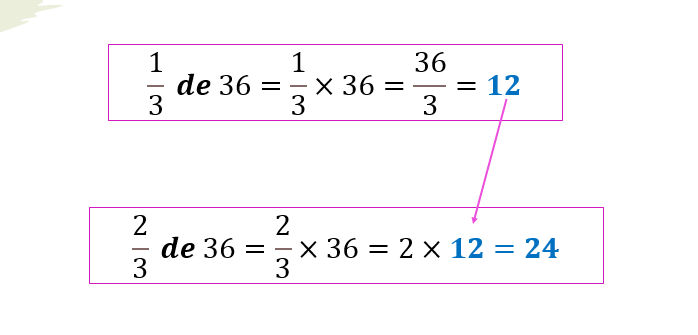
¿Te diste cuenta de que, al tener un tercio de 36 faltan dos tercios para completar el entero? Entonces, al dividir 36 entre 3 y multiplicar los 12 estudiantes que representaban un tercio por dos, obtuvieron como resultado 24 alumnos que son los dos tercios restantes.
Observas, así también así se puede resolver.
Es importante resaltar que para conocer qué parte de una cantidad es una fracción de ella, puedes dividir y multiplicar sucesivamente esa cantidad. Divide entre el denominador y multiplica por el numerador de la fracción.
Ahora trabaja con el problema 4

Problema 4. En la zona escolar hay 15 escuelas a las que asisten en total 3 760 alumnos, de los cuales 2 820 tienen más de dos hermanos. ¿Qué parte del total de alumnos tiene dos hermanos o menos?
Analiza la información que proporciona el problema:
15 escuelas.
3 760 estudiantes en total.
2 820 tienen más de 2 hermanos.
¿Qué parte del total de alumnos tiene dos hermanos o menos?
Una estrategia podría ser que se determine la razón entre el número de estudiantes que tienen dos hermanos y el total que hay en las 15 escuelas. Esto sería 2820 tienen más de dos hermanos de 3760 alumnos que hay en total.
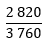
La relación que se presenta es correcta, hay que pensar cómo se puede utilizar para encontrar qué parte representa 2820 de 3760. Hay que buscar una fracción, un medio, o un tercio o un cuarto, según aplique.
Por ejemplo, en el problema anterior que acabas de resolver, la razón era que uno de tres o un tercio del total del grupo, eran menores de 10 años, y se buscaba una cantidad de estudiantes de 10 años o más.
Este problema puede verse al revés, dan las cantidades y hay que buscar las razones o fracciones.
Por eso es importante buscar que parte es 2820 de 3760 estudiantes.
Quizá hacer una división, pudiera ayudar a obtener el resultado.
Dibuja en tu cuaderno una tabla de dos columnas y cuatro filas.
En la primera fila, anota a la izquierda el número 1 y en la celda de la derecha, el total de los alumnos 3760
¿Sabes por qué te solicitan escribir el número 1?
Es uno porque la cantidad de estudiantes es el total, o sea, la unidad.
Con esto, ¿Ya te diste una idea de cómo se puede resolver el problema?
Puedes comenzar por dividir la cantidad.
¿Cómo aplicar la división? Puedes hacerlo con la calculadora y ve registrado los datos que obtengas.
Divide 3760 entre 2 lo cual te da 1880
Registra en la primera columna 1880 ¿Qué parte es 1880 de 3760?
Es un medio.
Registra un medio en la tabla, en la celda derecha.
Divide 1880 también entre 2 y te da 940
Registra 940
940 representa una cuarta parte de todos los niños.
Anota en la tabla, un cuarto.
Este dato sí sirve para lo que se necesita.
Al hacer una pequeña estimación con el 900 sucede que 900 por 3 es igual a 2700
Por tanto se encuentra que un cuarto de 3760 son 940 ¿Cómo se puede comprobar si es el dato que se necesita para encontrar la respuesta al problema?
Si multiplicas 940 por 2 da lo mismo que un medio = 1880 pero si multiplicas 940 por tres da: 2820 que es el número de niños que tienen 2 o menos hermanos.
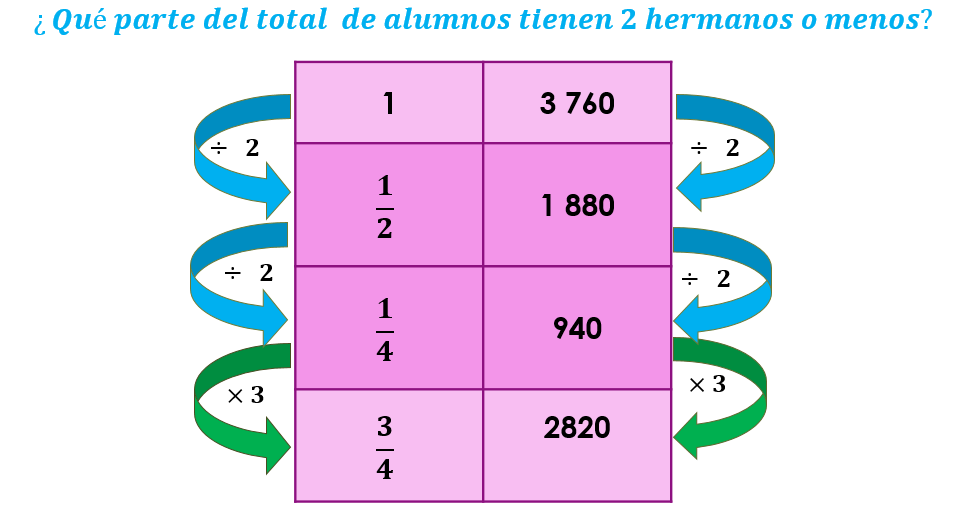
Observa la siguiente imagen que tiene lo que se acaba de hacer: al dividir la cantidad total de los alumnos, que es de 3760 en cuartos, es decir en 4 partes, obtienes que un cuarto de 3760 es 940 y si esta cantidad la multiplicas por tres y obtienes 2820 por lo tanto 3 cuartos de 3760 estudiantes son los que tienen dos hermanos o menos.
Hay otra forma de llegar a esa respuesta, ¿Cuál podría ser?
Prueba a dividir 2820 entre 3760 y registra ¿Qué obtienes?
El resultado es 0.75 que es equivalente a 3 cuartos también.
Esa es otra forma de obtener la respuesta. ¿Podrías calcular cuántos hombres de 15 años o más no saben leer ni escribir?

La población total de hombres mayores de 15 o más años es de 45 millones, 252 mil 363 y de ellos una veinticincoava parte no sabe leer ni escribir.

Son un millón 810 mil 095, hombres de 15 años o más que no saben leer ni escribir.
Sí que son muchas personas porque además falta considerar a las mujeres que están en esta misma condición.
El Reto de Hoy:
Investiga cuántas mujeres hay en México, de 15 años o más y cuántas de ellas no saben leer ni escribir. Comparte el trabajo realizado con algún familiar y explícale como resolviste los problemas, seguramente le parecerán muy interesantes y útiles.
Si en tu casa hay libros relacionados con el tema, consúltalos, así podrás saber más.
¡Buen trabajo!
Gracias por tu esfuerzo















Comentarios
Publicar un comentario